题目内容

在非直角△ABC中，向量
AB
|
AB
|cosB
+
AC
|
AC
|cosC
与向量
BC
的夹角为（　　）
分析：计算向量
AB
|
AB
|cosB
+
AC
|
AC
|cosC
与向量
BC
的数量积，得到数量积等于0，所以两向量的夹角是直角．
解答：解：∵(
AB
|
AB
|cosB
+
AC
|
AC
|cosC
)•
BC
=
AB
• 
BC
|
AB
|cosB
+
AC
•
BC
|
AC
|cosC

=
|
AB
|•
|BC
|cos(π-B)
|
AB
|cosB
+
|
AC
|•
|BC|cosC
|
AC
|cosC

=-|
BC
|+|
BC
|=0
∴向量
AB
|
AB
|cosB
+
AC
|
AC
|cosC
与向量
BC
垂直，
∴向量
AB
|
AB
|cosB
+
AC
|
AC
|cosC
与向量
BC
的夹角为直角．
故选B
点评：本题主要考查向量的数量积的计算，计算量较大，做题时要有耐心．
练习册系列答案
相关题目
在平面直角坐标系中，设三角形ABC 的顶点分别为A（0，a），B（b，0），C（c，0），点P（0，p）在线段OA上（异于端点），设a，b，c，p均为非零实数，直线BP，CP分别交AC，AB于点E，F，一同学已正确算得直线OF的方程：(
1
c
-
1
b
)x+(
1
p
-
1
a
)y=0，则OE的方程为：
（
1
b
-
1
c
）x+（
1
p
-
1
a
）y=0
（
1
b
-
1
c
）x+（
1
p
-
1
a
）y=0
．
在平面直角坐标系中，设三角形ABC 的顶点分别为A（0，a），B（b，0），C （c，0），点P（0，p）在线段AO 上（异于端点），设a，b，c，p 均为非零实数，直线BP，CP 分别交AC，AB 于点E，F，一同学已正确算得OE的方程：(
1
b
-
1
c
)x+(
1
p
-
1
a
)y=0，请你求OF的方程：
(
1
b
-
1
c
)x-(
1
p
-
1
a
)y=0
(
1
b
-
1
c
)x-(
1
p
-
1
a
)y=0
．
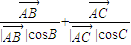在非直角△ABC中，向量与向量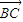的夹角为（ ）
A．锐角
B．直角
C．钝角
D．0
在非钝角△ABC中，已知3b=2asinB，且cosB=cosC，则△ABC的形状是
[     ]
A.等边三角形
B.等腰三角形
C.直角三角形
D.等腰直角三角形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网