Question

在平面直角坐标系中，设三角形ABC 的顶点分别为A（0，a），B（b，0），C（c，0），点P（0，p）在线段OA上（异于端点），设a，b，c，p均为非零实数，直线BP，CP分别交AC，AB于点E，F，一同学已正确算得直线OF的方程：(

1

c

-

1

b

)x+(

1

p

-

1

a

)y=0，则OE的方程为：

（

1

b

-

1

c

）x+（

1

p

-

1

a

）y=0

．

Answer 1

分析：因为点B与点C“地位平等”，所以它们具有可交换性，因此只要将直线OF方程中b与c交换，便可得直线OE方程中x的系数，确定出直线OE方程．

解答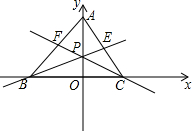：解：在平面直角坐标系中，三角形ABC的顶点分别为A（0，a），B（b，0），C（c，0），
∵点B与点C“地位平等”，
∴点B与点C具有可交换性，
∵OF的方程为（

1

c

-

1

b

）x+（

1

p

-

1

a

）y=0，
∴OE的方程为：（

1

b

-

1

c

）x+（

1

p

-

1

a

）y=0．
故答案为：（

1

b

-

1

c

）x+（

1

p

-

1

a

）y=0

点评：此题考查了直线的一般式方程，主要体现了“对称轮换思想”，灵活运用此思想是解本题的关键．