题目内容
已知f(n)=1+ +
+ +…+
+…+ (n∈N*),用数学归纳法证明f(2n)>
(n∈N*),用数学归纳法证明f(2n)> 时,f(2k+1)-f(2k)等于 .
时,f(2k+1)-f(2k)等于 .
 +
+ +…+
+…+ (n∈N*),用数学归纳法证明f(2n)>
(n∈N*),用数学归纳法证明f(2n)> 时,f(2k+1)-f(2k)等于 .
时,f(2k+1)-f(2k)等于 . +
+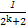 +…+
+…+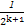
f(2k+1)-f(2k)
=1+ +
+ +…+
+…+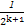 -(1+
-(1+ +
+ +…+
+…+ )
)
= +
+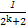 +…+
+…+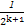 .
.
=1+
 +
+ +…+
+…+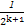 -(1+
-(1+ +
+ +…+
+…+ )
)=
 +
+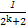 +…+
+…+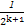 .
.
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
题目内容
 +
+ +…+
+…+ (n∈N*),用数学归纳法证明f(2n)>
(n∈N*),用数学归纳法证明f(2n)> 时,f(2k+1)-f(2k)等于 .
时,f(2k+1)-f(2k)等于 . +
+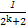 +…+
+…+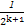
 +
+ +…+
+…+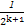 -(1+
-(1+ +
+ +…+
+…+ )
) +
+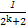 +…+
+…+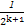 .
.
 优加精卷系列答案
优加精卷系列答案