题目内容

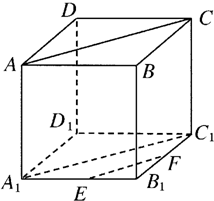
在正方体ABCD-A1B1C1D1中，E，F分别是线段A1B1，B1C1上的不与端点重合的动点，如果A1E=B1F，有下面四个结论：
①EF⊥AA1；②EF∥AC；③EF与AC异面；④EF∥平面ABCD．其中一定正确的有（　　）
A．①②B．②③C．②④D．①④
如图所示．由于AA1⊥平面A1B1C1D1，EF?平面A1B1C1D1，
则EF⊥AA1，所以①正确；
当E，F分别不是线段A1B1，B1C1的中点时，EF与AC异面，
所以②不正确；
当E，F分别是线段A1B1，B1C1的中点时，EF∥A1C1，又AC∥A1C1，
则EF∥AC，所以③不正确；
由于平面A1B1C1D1∥平面ABCD，EF?平面A1B1C1D1，
所以EF∥平面ABCD，所以④正确．
故选D．
练习册系列答案
相关题目
已知M＞-3，设命题p：曲线
x2
2
+
y2
m+3
=1表示焦点在y轴上的椭圆，命题q：当0＜x＜2时，函数f（x）=x+
1
x
＞m恒成立．
（Ⅰ）若“p∧q”为真命题，求m的取值范围；
（Ⅱ）若“p∨q”为真命题，“p∧q”为假命题，求m的取值范围．
对于两个复数α=-
1
2
+
3
2
i，β=-
1
2
-
3
2
i，有下列四个结论：①αβ=1；②
α
β
=1；③
|α|
|β|
=1；④α3+β3=1，其中正确的结论的个数为（　　）
A．1B．2C．3D．4
下列命题中错误的是（　　）
A．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β
B．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面β
C．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面β
D．如果平面α⊥平面γ，平面γ⊥平面β，α∩β=l，则l⊥γ
已知函数y=f（x）的导函数y=f'（x）的图象如图所示，给出如下命题：
①0是函数y=f（x）的一个极值点；
②函数y=f（x）在x=-
1
2
处切线的斜率小于零；
③f（-1）＜f（0）；
④当-2＜x＜0时，f（x）＞0．
其中正确的命题是______．（写出所有正确命题的序号）
已知命题p：“函数f（x）=2x和g（x）=（
1
2
）x的图象关于y轴对称”，则￢p是______命题；（填“真”或“假”）
已知命题p：任意x∈R，x2+1≥a，命题q：函数f（x）=x2-2ax+1在（-∞，-1]上单调递减．
（1）若命题p为真命题，求实数a的取值范围；
（2）若p和q均为真命题，求实数a的取值范围．
下列语句中是简单命题是（　　）
A．
3
不是有理数		B．△ABC是等腰直角三角形
C．负数的平方是正数D．3x+2＜0
下列命题：
①直线y=2x在x，y轴上的截距相等；
②参数方程
x=3sinα
y=3cosα
(α为参数）表示圆；
③世界上第一个把π计算到3.1415926＜π＜3.1415927的人是中国人刘徽；
④抛两枚均匀的骰子，恰好出现一奇一偶的概率为
1
4
；
⑤满足||PF1|-|PF2||=2a（a＞0）的动点P的轨迹是双曲线．
其中错误的命题的序号是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网