题目内容
设函数 f (x)=ax-lnx-3(a∈R),g(x)=xe1-x.
(Ⅰ)若函数 g(x) 的图象在点 (0,0) 处的切线也恰为 f (x) 图象的一条切线,求实数 a的值;
(Ⅱ)是否存在实数a,对任意的 x∈(0,e],都有唯一的 x0∈[e-4,e],使得 f (x0)=g(x) 成立.若存在,求出a的取值范围;若不存在,请说明理由.
注:e是自然对数的底数.
【答案】
解:(1)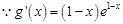 ,
,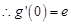 ,所以
,所以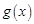 的图象在
的图象在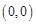 处的切线方程是
处的切线方程是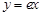 ;2分
;2分
设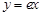 与
与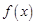 的图象切于点
的图象切于点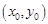 ,而
,而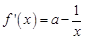 ,
,
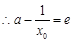 且
且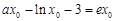 ,解得
,解得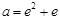 ; 5分
; 5分
(2)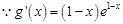 ,
,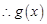 在
在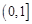 上单调递增,在
上单调递增,在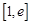 上单调递减,
上单调递减,
且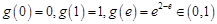 ,
,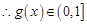 ; 8分
; 8分
若令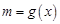 ,则原命题等价于对于任意
,则原命题等价于对于任意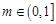 ,都有唯一的
,都有唯一的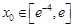 ,使得
,使得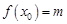 成立.
9分
成立.
9分
而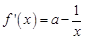 ,
, ,
,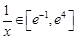
①当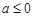 时,
时,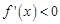 恒成立,所以
恒成立,所以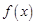 在
在 上单调递减,要满足条件,则必须有
上单调递减,要满足条件,则必须有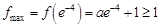 ,且
,且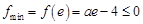 ,无解,所以此时不存在满足条件的
,无解,所以此时不存在满足条件的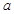 ;10分
;10分
②当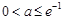 ,
,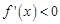 恒成立,所以
恒成立,所以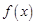 在
在 上单调递减,要满足条件,则必须有
上单调递减,要满足条件,则必须有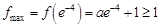 ,且
,且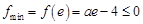 ,解得
,解得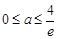 ,
,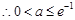 ;11分
;11分
③当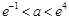 时,
时,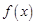 在区间
在区间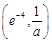 上单调递减,在
上单调递减,在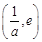 上单调递增,
上单调递增,
又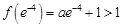 ,要满足条件,则
,要满足条件,则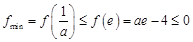 ,解得
,解得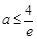 ,
,
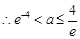 ; 12分
; 12分
④当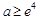 时,
时,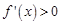 恒成立,所以
恒成立,所以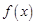 在
在 上单调递增,
上单调递增,
又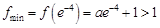 ,所以此时不存在
,所以此时不存在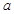 满足条件; 13分
满足条件; 13分
综上有 . 15分
. 15分
【解析】略

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 x3-
x3- x2+a x.
x2+a x. -6x+5,X
-6x+5,X R
R