题目内容
9.若不等式x2+2$\sqrt{2}$xy≤a(x2+y2)对于一切正数x,y恒成立,则实数a的最小值为2.分析 x2+2$\sqrt{2}$xy≤a(x2+y2)?(a-1)($\frac{x}{y}$)2-2$\sqrt{2}$×$\frac{x}{y}$+a≥0,对于一切正数x,y恒成立,依题意,令f(t)=(a-1)t2-2t+a,列不等式组$\left\{\begin{array}{l}{a-1>0}\\{f(\frac{\sqrt{2}}{a-1})≥0}\end{array}\right.$,解之即可得答案.
解答 解:∵x>0,y>0,
∴x2+2$\sqrt{2}$xy≤a(x2+y2)?(a-1)($\frac{x}{y}$)2-2$\sqrt{2}$×$\frac{x}{y}$+a≥0,
令t=$\frac{x}{y}$(t>0),f(t)=(a-1)t2-2$\sqrt{2}$t+a,
依题意,$\left\{\begin{array}{l}{a-1>0}\\{f(\frac{\sqrt{2}}{a-1})≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{a>1}\\{a-\frac{2}{a-1}≥0}\end{array}\right.$,解得a≥2.
∴实数a的最小值为2.
故答案为:2
点评 本题考查函数恒成立问题,考查转化与构造函数思想,考查解不等式组的能力,属于难题.

练习册系列答案
相关题目
 如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.
如图1,已知四边形ABCD的对角线AC与BD互相垂直,∠A=60°,∠C=90°,CD=CB=2,将△ABD沿BD折起,得到三棱锥A′-BCD,如图2.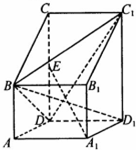 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,AB∥CD,AD⊥CD,侧棱AA1⊥底面ABCD,E是CD的中点,CD=2AB=2AD,AD=1,AA1=$\sqrt{2}$.
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,AB∥CD,AD⊥CD,侧棱AA1⊥底面ABCD,E是CD的中点,CD=2AB=2AD,AD=1,AA1=$\sqrt{2}$. 如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为 $\frac{2}{9}$.
如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为 $\frac{2}{9}$.