Question

14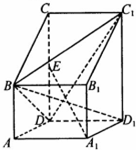．如图，已知四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是直角梯形，AB∥CD，AD⊥CD，侧棱AA₁⊥底面ABCD，E是CD的中点，CD=2AB=2AD，AD=1，AA₁=$\sqrt{2}$．
（1）求证：EA₁⊥BD；
（2）求三棱锥D-BD₁C₁的体积．

Answer 1

分析 （1）如图所示，连接BE，AE，由已知可得：四边形ADEB是正方形，可得BD⊥AE，利用直棱柱的性质可得AA₁⊥BD，可得BD⊥平面AEA₁，即可证明；
（2）利用${V}_{D-B{D}_{1}{C}_{1}}$=${V}_{B-D{D}_{1}{C}_{1}}$即可得出．

解答 （1）证明：如图所示，连接BE，AE，
∵E是CD的中点，CD=2AB=2AD，∠BAD=Rt∠，
∴四边形ADEB是正方形，
∴BD⊥AE，
又AA₁⊥平面ABCD，
∴AA₁⊥BD，
又AE∩AA₁=A，
∴BD⊥平面AEA₁，
∴EA₁⊥BD；
（2）解：${S}_{△D{D}_{1}{C}_{1}}$=$\frac{1}{2}D{D}_{1}×{D}_{1}{C}_{1}$=$\frac{1}{2}×\sqrt{2}×2$=$\sqrt{2}$．
∴${V}_{D-B{D}_{1}{C}_{1}}$=${V}_{B-D{D}_{1}{C}_{1}}$=$\frac{1}{3}×BE×{S}_{△D{D}_{1}{C}_{1}}$=$\frac{1}{3}×1×\sqrt{2}$=$\frac{\sqrt{2}}{3}$．

点评 本题考查了直棱柱的性质、正方形的性质、线面垂直的判定与性质定理、三棱锥的体积计算公式、三角形的面积计算公式，考查了推理能力与计算能力，属于中档题．