题目内容
18. 如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为 $\frac{2}{9}$.
如图,∠ACB=90°,DA⊥平面ABC,AE⊥DB交DB于E,AF⊥DC交DC于F,且AD=AB=2,则三棱锥D-AEF体积的最大值为 $\frac{2}{9}$.
分析 要求三棱锥D-AEF体积的最大值,由题意可得:DE⊥平面AEF,且DE=$\sqrt{2}$.因此只有求出Rt△AEF面积的最大值即可.
解答 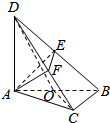 解:∵DA⊥平面ABC,
解:∵DA⊥平面ABC,
∴DA⊥AB,AD⊥BC.
∵AE⊥BD,又AD=AB=2,
∴DE=$\sqrt{2}$.
又BC⊥AC,AC∩AD=A,
∴BC⊥平面ACD.
∴平面BCD⊥平面ACD,
∵AF⊥CD,平面BCD∩平面ACD=CD,
∴AF⊥平面BCD.
∴AF⊥EF,BD⊥EF.
∴BD⊥平面AEF.
由AF2+EF2=AE2=2≥2AF•EF,
∴AF•EF≤1.
∴S△AEF≤$\frac{1}{2}×1$=$\frac{1}{2}$.
∴则三棱锥D-AEF体积的最大值为$\frac{1}{3}×\sqrt{2}×\frac{1}{2}$=$\frac{\sqrt{2}}{6}$.
故答案为:$\frac{\sqrt{2}}{6}$.
点评 本题考查了线面垂直的判定与性质定理、三棱锥的体积计算公式、三角形的面积计算公式、三角形相似的性质、圆的性质、射影定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
6.在△ABC中,内角A,B,C的对边分别为a,b,c(b≠1),且$\frac{C}{A}$,$\frac{sinB}{sinA}$都是方程log${\;}_{\sqrt{b}}$x=logb(4x-4)的根,则△ABC中最大的角是( )
| A. | 135° | B. | 120° | C. | 90° | D. | 150° |
13.曲线y=e${\;}^{\frac{1}{2}x}$在点(4,e2)处的切线的纵截距为( )
| A. | -e2 | B. | -4e2 | C. | 2e2 | D. | $\frac{9}{2}$e2 |
 直三棱柱ABC-A1B1C1中,AB=10,AC=8,BC=6,AA1=8,点D在线段AB上.
直三棱柱ABC-A1B1C1中,AB=10,AC=8,BC=6,AA1=8,点D在线段AB上.