题目内容
已知函数y=lg( -x),求其定义域,并判断其奇偶性、单调性.
-x),求其定义域,并判断其奇偶性、单调性.
 -x),求其定义域,并判断其奇偶性、单调性.
-x),求其定义域,并判断其奇偶性、单调性.由题意 -x>0,解得x∈R,即定义域为R.
-x>0,解得x∈R,即定义域为R.
又f(-x)=lg[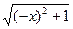 -(-x)]=lg(
-(-x)]=lg( +x)=lg
+x)=lg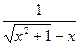 =lg(
=lg( -x)-1=-lg(
-x)-1=-lg( -x)=-f(x),∴y=lg(
-x)=-f(x),∴y=lg( -x)是奇函数.任取x1、x2∈(0,+∞)且x1<x2,
-x)是奇函数.任取x1、x2∈(0,+∞)且x1<x2,
则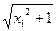 <
<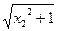
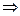
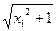 +x1<
+x1<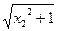 +x2
+x2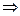
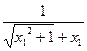 >
>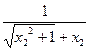 ,
,
即有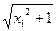 -x1>
-x1>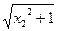 -x2>0,
-x2>0,
∴lg(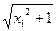 -x1)>lg(
-x1)>lg(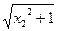 -x2),即f(x1)>f(x2)成立.
-x2),即f(x1)>f(x2)成立.
∴f(x)在(0,+∞)上为减函数.
又f(x)是定义在R上的奇函数,故f(x)在(-∞,0)上也为减函数.
 -x>0,解得x∈R,即定义域为R.
-x>0,解得x∈R,即定义域为R.又f(-x)=lg[
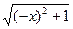 -(-x)]=lg(
-(-x)]=lg( +x)=lg
+x)=lg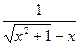 =lg(
=lg( -x)-1=-lg(
-x)-1=-lg( -x)=-f(x),∴y=lg(
-x)=-f(x),∴y=lg( -x)是奇函数.任取x1、x2∈(0,+∞)且x1<x2,
-x)是奇函数.任取x1、x2∈(0,+∞)且x1<x2,则
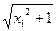 <
<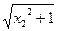
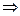
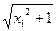 +x1<
+x1<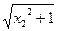 +x2
+x2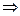
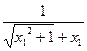 >
>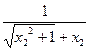 ,
,即有
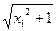 -x1>
-x1>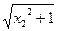 -x2>0,
-x2>0,∴lg(
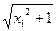 -x1)>lg(
-x1)>lg(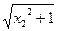 -x2),即f(x1)>f(x2)成立.
-x2),即f(x1)>f(x2)成立.∴f(x)在(0,+∞)上为减函数.
又f(x)是定义在R上的奇函数,故f(x)在(-∞,0)上也为减函数.
注意到 +x=
+x=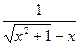 ,即有lg(
,即有lg( -x)=-lg(
-x)=-lg( +x),从而f(-x)=lg(
+x),从而f(-x)=lg( +x)=-lg(
+x)=-lg( -x)=-f(x),可知其为奇函数.又因为奇函数在关于原点对称的区间上的单调性相同,所以我们只需研究(0,+∞)上的单调性.
-x)=-f(x),可知其为奇函数.又因为奇函数在关于原点对称的区间上的单调性相同,所以我们只需研究(0,+∞)上的单调性.
 +x=
+x=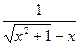 ,即有lg(
,即有lg( -x)=-lg(
-x)=-lg( +x),从而f(-x)=lg(
+x),从而f(-x)=lg( +x)=-lg(
+x)=-lg( -x)=-f(x),可知其为奇函数.又因为奇函数在关于原点对称的区间上的单调性相同,所以我们只需研究(0,+∞)上的单调性.
-x)=-f(x),可知其为奇函数.又因为奇函数在关于原点对称的区间上的单调性相同,所以我们只需研究(0,+∞)上的单调性.
练习册系列答案
相关题目
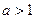 ,若仅有一个常数c使得对于任意的
,若仅有一个常数c使得对于任意的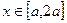 ,都有
,都有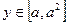 满足方程
满足方程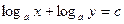 ,这时,
,这时, 的取值的集合为 .
的取值的集合为 .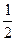 )
)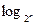 3n)×log9
3n)×log9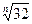 =________________.
=________________.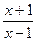 +log2(x-1)+log2(p-x)的值域.
+log2(x-1)+log2(p-x)的值域.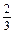 与log5
与log5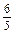 ;
;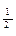 b<log
b<log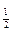 a<log
a<log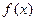 为定义在
为定义在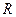 上的偶函数,当时,
上的偶函数,当时,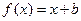 ,且
,且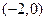 ,又在
,又在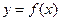 的图象中,另一部分是顶点在(0,2),且过点(-1,1)的一段抛物线,试写出函数
的图象中,另一部分是顶点在(0,2),且过点(-1,1)的一段抛物线,试写出函数 ,求
,求
 最大值和最小值.
最大值和最小值.