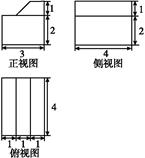
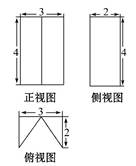
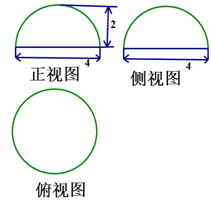
题目内容
如图,四边形ABCD中,AB=AD=CD=1,BD=
,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )
(A)A'C⊥BD
(B)∠BA'C=90°
(C)CA'与平面A'BD所成的角为30°
(D)四面体A'-BCD的体积为
,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A'-BCD,使平面A'BD⊥平面BCD,则下列结论正确的是( )(A)A'C⊥BD
(B)∠BA'C=90°
(C)CA'与平面A'BD所成的角为30°
(D)四面体A'-BCD的体积为
B
折叠前AB=AD=1,BD=,即AB⊥AD,折叠后平面A'BD⊥平面BCD,且CD⊥BD,故CD⊥平面A'BD.
取BD的中点O,∵A'B=A'D,
∴A'O⊥BD.又平面A'BD⊥平面BCD,平面A'BD∩平面BCD=BD,
∴A'O⊥平面BCD.
∵CD⊥BD,
∴OC不垂直于BD.假设A'C⊥BD,
∵OC为A'C在平面BCD内的射影,
∴OC⊥BD,矛盾,∴A'C不垂直于BD,A错误;
∵CD⊥BD,平面A'BD⊥平面BCD,
∴CD⊥平面A'BD,A'C在平面A'BD内的射影为A'D.
∵A'B=A'D=1,BD=,
∴A'B⊥A'D,A'B⊥A'C,B正确;∠CA'D为直线CA'与平面A'BD所成的角,
∠CA'D=45°,C错误;
VA'-BCD=VC-A'BD=S△A'BD·CD=
,D错误.
,即AB⊥AD,折叠后平面A'BD⊥平面BCD,且CD⊥BD,故CD⊥平面A'BD.取BD的中点O,∵A'B=A'D,
∴A'O⊥BD.又平面A'BD⊥平面BCD,平面A'BD∩平面BCD=BD,
∴A'O⊥平面BCD.
∵CD⊥BD,
∴OC不垂直于BD.假设A'C⊥BD,
∵OC为A'C在平面BCD内的射影,
∴OC⊥BD,矛盾,∴A'C不垂直于BD,A错误;
∵CD⊥BD,平面A'BD⊥平面BCD,
∴CD⊥平面A'BD,A'C在平面A'BD内的射影为A'D.
∵A'B=A'D=1,BD=
,∴A'B⊥A'D,A'B⊥A'C,B正确;∠CA'D为直线CA'与平面A'BD所成的角,
∠CA'D=45°,C错误;
VA'-BCD=VC-A'BD=
S△A'BD·CD=,D错误.
练习册系列答案
相关题目
