题目内容
10.已知函数f(x)=$\sqrt{3}$sin2x-2cos2x+1.(1)若x∈R,求f(x)的单调增区间;
(2)若x∈[0,$\frac{π}{2}$],求f(x)的最大值和最小值.
分析 (1)由条件利用三角恒等变换化简函数的解析式,再利用正弦函数的单调性,求得函数f(x)的增区间.
(2)由题意利用正弦函数的定义域和值域,求得f(x)的最大值和最小值.
解答 解:(1)函数f(x)=$\sqrt{3}$sin2x-2cos2x+1=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$),
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,
故函数f(x)的增区间为[kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z.
(2)若x∈[0,$\frac{π}{2}$],则2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],故当2x-$\frac{π}{6}$=-$\frac{π}{6}$时,函数f(x)取得最小值为-1;
当2x-$\frac{π}{6}$=$\frac{π}{2}$时,函数f(x)取得最大值为2.
点评 本题主要考查三角恒等变换,正弦函数的单调性,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
18.如图,半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的体积与该圆柱的体积之比是( )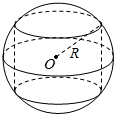

| A. | $\frac{4}{3}$ | B. | $\frac{4\sqrt{2}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
5.已知正项数列{an}的前n项和为Sn,若4Sn2-2=an2+$\frac{1}{{a}_{n}^{2}}$(n∈N*),则S2015=( )
| A. | 2015+$\frac{\sqrt{2015}}{2015}$ | B. | 2015-$\frac{\sqrt{2015}}{2015}$ | C. | 2015 | D. | $\sqrt{2015}$ |
20.依法纳税是每个公民应尽的义务,国家征收个人工资、薪金所得税是分段计算的:总收入不超过3500元,免征个人工资、薪金所得税;超过3500元的部分需征税,设全月应纳税额(所得额指工资、薪金中应纳税的部分)为x,x=(全月总收入-“三险一金”-扣除数)元,税率如表所示:
(1)若应纳税所得额为f(x),试用分段函数表示1~3级纳税额f(x)的计算公式;
(2)某单位按工资额的19%为其职工缴纳“三险一金”(养老保险8%、医疗保险2%、失业保险1%、住房公积金8%),2014年1月份该单位某职工缴税40.8元,请问该职工该月总收入多少元?
| 级 数 | 全月应纳税所得额x | 税 率 |
| 1 | 不超过1500元的部分 | 3% |
| 2 | 超过1500元至4500元的部分 | 10% |
| 3 | 超过4500元至9000元的部分 | 20% |
| 4 | 超过9000元至35000元的部分 | 25% |
| 5 | 超过35000元至55000元的部分 | 30% |
| 6 | 超过55000元至80000元的部分 | 35% |
| 7 | 超过80000元的部分 | 45% |
(2)某单位按工资额的19%为其职工缴纳“三险一金”(养老保险8%、医疗保险2%、失业保险1%、住房公积金8%),2014年1月份该单位某职工缴税40.8元,请问该职工该月总收入多少元?
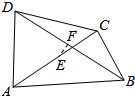 如图,在空间四边形ABCD中,连接AC,BD,E,F分别是边AC.BD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$-2$\overrightarrow{c}$,$\overrightarrow{CD}$=5$\overrightarrow{a}$+6$\overrightarrow{b}$-8$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{EF}$.
如图,在空间四边形ABCD中,连接AC,BD,E,F分别是边AC.BD的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$-2$\overrightarrow{c}$,$\overrightarrow{CD}$=5$\overrightarrow{a}$+6$\overrightarrow{b}$-8$\overrightarrow{c}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示$\overrightarrow{EF}$.