题目内容
若关于x的方程x-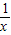
+k=0在x∈（0，1）没有实数根，则k的取值范围为 ．
【答案】分析：构建函数f（x）=-k=x-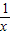
，将方程有无根问题转化为图象的交点的个数问题．
解答：解：令f（x）=-k=x-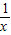
，显然f（x）在区间上单调递增，则f（x）＜0，要使方程在指定区域无实根，必有-k≥0，得k≤0
故答案为 k≤0．
点评：本题主要考查方程根的个数的判断，考查函数与方程的思想，属于基础题．
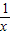，将方程有无根问题转化为图象的交点的个数问题．解答：解：令f（x）=-k=x-
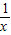，显然f（x）在区间上单调递增，则f（x）＜0，要使方程在指定区域无实根，必有-k≥0，得k≤0故答案为 k≤0．
点评：本题主要考查方程根的个数的判断，考查函数与方程的思想，属于基础题．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
若关于x的方程ax+2x-4=0（a＞0且a≠1）的所有根记作x1，x2，…，xm（m∈N*），关于x的方程loga2x+x-2=0的所有根记作x1′，x2′，…，xn′（n∈N*），则
的值为（ ）
x1+x2+…+xm+
| ||||||
| m+n |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
若关于x的方程x|x-a|=a有三个不相同的实根，则实数a的取值范围为（ ）
| A、（0，4） | B、（-4，0） | C、（-∞，-4）∪（4，+∞） | D、（-4，0）∪（0，4） |