题目内容
已知函数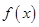 的定义域为
的定义域为 ,部分对应值如表,
,部分对应值如表,
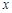 | -1 | 0 | 2 | 4 | 5 |
 | 1 | 2 | 1 | 2 | 1 |
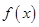 的导函数
的导函数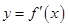 的图象如图所示.
的图象如图所示. 
下列关于
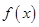 的命题:
的命题:①函数
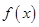 的极大值点为
的极大值点为 ,
,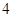 ;
;②函数
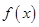 在
在 上是减函数;
上是减函数;③当
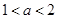 时,函数
时,函数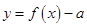 有
有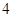 个零点;
个零点;④函数
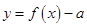 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个.其中正确命题的序号是 .
???
解析试题分析:先由导函数的图象和原函数的关系画出原函数的大致图象,再借助与图象和导函数的图象,对五个命题,一一进行验证,对于假命题采用举反例的方法进行排除即可得到答案.解:由导函数的图象和原函数的关系得,原函数的大致图象可由以下两种代表形式,如图: 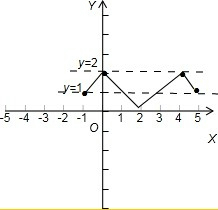
由图得:①由图象可知f′(2)=0,f(x)在x=0,4处取得极大值,故①正确
②因为在[0,2]上导函数为负,故原函数递减,故②正确;
③当a离1非常接近时,对于上图,y=f(x)-a的零点,就是y与f(x)=a的交点个数,图有2个零点,也可以是3个零点,故③错误.
④函数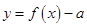 的零点个数可能为0、1、2、3、4个,不会有三个,故错误。
的零点个数可能为0、1、2、3、4个,不会有三个,故错误。
综上得:真命题只有???.故答案为:???;
考点:导函数和原函数的单调性的关系
点评:本题主要考查导函数和原函数的单调性之间的关系.二者之间的关系是:导函数为正,原函数递增;导函数为负,原函数递减.

练习册系列答案
相关题目

 与直线
与直线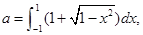 则
则 展开式中的常数项为 ;
展开式中的常数项为 ;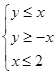 表示的平面区域为
表示的平面区域为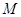 ,直线
,直线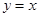 与曲线
与曲线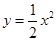 所围成的平面区域为
所围成的平面区域为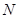 ,现随机向区域
,现随机向区域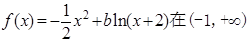 上是减函数,则
上是减函数,则 的取值范围是 __.
的取值范围是 __.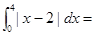 _________
_________ 在点
在点 处的切线与两坐标轴围成的三角形的面积是 。
处的切线与两坐标轴围成的三角形的面积是 。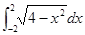 =___________
=___________ 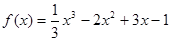 的单调递增区间为____________.
的单调递增区间为____________.