题目内容
5.设0<a<1,函数f(x)=logax+log${\;}_{\frac{1}{a}}$(2-x),则函数f-1(x)<1的x的取值范围是( )| A. | (0,2) | B. | (2,+∞) | C. | (0,+∞) | D. | (loga(2-a),+∞) |
分析 先确定函数f(x)=logax+log${\;}_{\frac{1}{a}}$(2-x)的定义域为(0,2),值域为R;从而求出f-1(x)=$\frac{2•{a}^{x}}{{a}^{x}+1}$,从而解得.
解答 解:函数f(x)=logax+log${\;}_{\frac{1}{a}}$(2-x)的定义域为(0,2),值域为R;
f(x)=logax+log${\;}_{\frac{1}{a}}$(2-x)=loga$\frac{x}{2-x}$=y,
∴x=$\frac{2{a}^{y}}{{a}^{y}+1}$,
故f-1(x)=$\frac{2•{a}^{x}}{{a}^{x}+1}$,
∴$\frac{2•{a}^{x}}{{a}^{x}+1}$-1<0,
即0<ax<1,又∵0<a<1,
∴x>0,
故选:C.
点评 本题考查了反函数的应用及不等式的解法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知椭圆C:$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,点M与C的焦点不重合,若M关于C的焦点的对称点分别为A,B,线段MN的中点在C上,则|AN|+|BN|=( )
| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
15.设全集U=R,M={x|y=2x+1},N={y|y=-x2},则M和N的关系是( )
| A. | M$\underset{?}{≠}$N | B. | M∩N={(-1,1)} | C. | M=N | D. | N$\underset{?}{≠}$M |
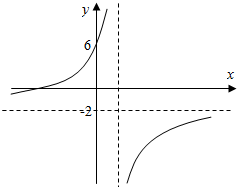 已知函数f(x)=$\frac{2x+b}{x-a}$(x∈R,x≠a).
已知函数f(x)=$\frac{2x+b}{x-a}$(x∈R,x≠a).