题目内容
在△ABC中，D是BC的中点，E是DC的中点，若
=
，
=
，则
=（ ）
| AB |
| a |
| AC |
| b |
| AE |
分析：根据D是BC的中点，E是DC的中点，可得
=
+
=
，用向量减法的意义，变形得
-
=
(
-
)，整理即可得到
=
+
，找到正确答案．
| BE |
| BD |
| DE |
| 3 |
| 4 |
| BC |
| AE |
| AB |
| 3 |
| 4 |
| AC |
| AB |
| AE |
| 1 |
| 4 |
| a |
| 3 |
| 4 |
| b |
解答：解：∵D是BC的中点，
∴
=
=
又∵E是DC的中点，
∴
=
=
，可得
=
+
=
∵
=
-
，
=
-
∴
-
=
(
-
)，可得
=
+
∵
=
，
=
，
∴
=
+
故选B
∴
| BD |
| DC |
| 1 |
| 2 |
| BC |
又∵E是DC的中点，
∴
| DE |
| 1 |
| 2 |
| DC |
| 1 |
| 4 |
| BC |
| BE |
| BD |
| DE |
| 3 |
| 4 |
| BC |
∵
| BE |
| AE |
| AB |
| BC |
| AC |
| AB |
∴
| AE |
| AB |
| 3 |
| 4 |
| AC |
| AB |
| AE |
| 1 |
| 4 |
| AB |
| 3 |
| 4 |
| AC |
∵
| AB |
| a |
| AC |
| b |
∴
| AE |
| 1 |
| 4 |
| a |
| 3 |
| 4 |
| b |
故选B
点评：本题在三角形一边上定点分该边的比已知的情况下，要求用两个向量作为基向量表示第三个向量，考查了向量的线性运算、平面向量的基本定理等知识点，属于基础题．
练习册系列答案
步步高达标卷系列答案
相关题目
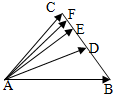如图，在△ABC中，D是BC的中点，E是DC的中点，F是EC的中点，若| AB |
| a |
| AC |
| b |
| AF |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
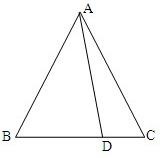如图，在△ABC中，D是BC边上的任一点（D与B，C不重合），
请考生在第（1），（2），（3）题中任选一题作答，如果多做，则按所做的第一题记分．