题目内容
在△ABC中，D是BC边上一点，BD=3DC，若P是AD边上一动点，AD=2
（Ⅰ）设
=
，
=
，用
，
表示向量
（Ⅱ）求
•(
+3
)的最小值．
（Ⅰ）设
| PB |
| a |
| PC |
| b |
| a |
| b |
| PD |
（Ⅱ）求
| PA |
| PB |
| PC |
分析：（I）先分别利用
，
表示
，
，然后结合
=3
，代入即可求解
（II）由（Ⅰ）可知
+3
=4
，先|
|=x(0≤x≤2)，代入利用向量的数量积的定义及二次函数的性质即可求解
| PD |
| PB |
| BD |
| CD |
| BD |
| DC |
（II）由（Ⅰ）可知
| PB |
| PC |
| PD |
| PA |
解答：解：（Ⅰ）依题
=
-
，
=
-
又
=-3
所以
-
=-3(
-
)
整理可得4
=
+3
则
=
+
（Ⅱ）由（Ⅰ）可知
+3
=4
设|
|=x(0≤x≤2)故
•(
+3
)=
•(4
)=-4x（2-x）≥-4
所以当x=1时
•(
+3
)的最小值为-4
| BD |
| PD |
| PB |
| CD |
| PD |
| PC |
又
| BD |
| CD |
| PD |
| PB |
| PD |
| PC |
整理可得4
| PD |
| PB |
| PC |
| PD |
| 1 |
| 4 |
| a |
| 3 |
| 4 |
| b |
（Ⅱ）由（Ⅰ）可知
| PB |
| PC |
| PD |
设|
| PA |
| PA |
| PB |
| PC |
| PA |
| PD |
所以当x=1时
| PA |
| PB |
| PC |
点评：本题主要考查了向量的数量积的定义及向量的基本运算的简单应用，解题时要准确利用基本公式
练习册系列答案
相关题目
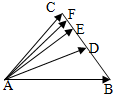如图，在△ABC中，D是BC的中点，E是DC的中点，F是EC的中点，若| AB |
| a |
| AC |
| b |
| AF |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
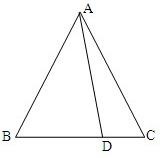如图，在△ABC中，D是BC边上的任一点（D与B，C不重合），
请考生在第（1），（2），（3）题中任选一题作答，如果多做，则按所做的第一题记分．