题目内容
已知等比数列{an}的公比为q,Sn是{an}的前n项和.
(1)若a1=1,q>1,求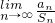 的值;
的值;
(2)若a1=1;对① 和②
和②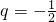 时,分别研究Sn的最值,并说明理由;
时,分别研究Sn的最值,并说明理由;
(3)若首项a1=10,设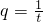 ,t是正整数,t满足不等式|t-63|<62,且对于任意正整数n有9<Sn<12成立,问:这样的数列{an}有几个?
,t是正整数,t满足不等式|t-63|<62,且对于任意正整数n有9<Sn<12成立,问:这样的数列{an}有几个?
解:(1)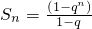 ,则
,则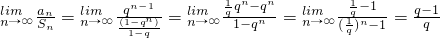 ----(5分)
----(5分)
(2)当 时,
时,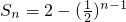 ,所以Sn随n的增大而增大,而S1≤Sn<2,
,所以Sn随n的增大而增大,而S1≤Sn<2,
此时Sn有最小值为1,但无最大值.-------------------------------(3分)
(只给出答案而不能够说明理由的,得1分)
当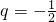 时,
时,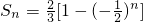
若n=2k,k∈N*时,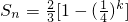 ,所以Sn随k的增大而增大,
,所以Sn随k的增大而增大,
即n是偶数时,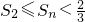 ,即
,即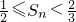
若n=2k-1,k∈N*时,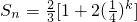 ,所以Sn随k的增大而减小,
,所以Sn随k的增大而减小,
即n是奇数时,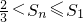 ,即
,即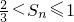
所以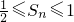 ,Sn有最大值为1,最小值为
,Sn有最大值为1,最小值为 .---(4分)
.---(4分)
(只给出答案而不能够说明理由的,得1分)
(3)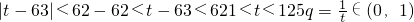 .
.
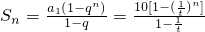 且Sn随着n的增大而增大
且Sn随着n的增大而增大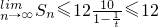 -----------------------(3分)
-----------------------(3分)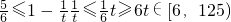 -----------------------------(2分)
-----------------------------(2分)
t∈N*?124-6+1=119个.----------------------------------------(1分)
分析:(1)利用等比数列的求和公式,进而可求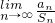 的值;
的值;
(2)当 时,
时,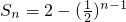 ,所以Sn随n的增大而增大,而S1≤Sn<2,此时Sn有最小值为1,但无最大值当
,所以Sn随n的增大而增大,而S1≤Sn<2,此时Sn有最小值为1,但无最大值当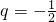 时,
时,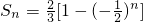 ,分n是偶数,奇数讨论求最大值与最小值
,分n是偶数,奇数讨论求最大值与最小值
(3)根据t满足不等式|t-63|<62,可确定q的范围,进而可得Sn随着n的增大而增大,利用9<Sn<12,可求解.
点评:本题以等比数列为载体,考查数列的极限,考查等比数列的求和,考查数列的单调性,属于中档题.
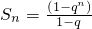 ,则
,则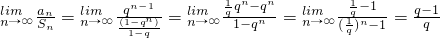 ----(5分)
----(5分)(2)当
 时,
时,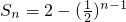 ,所以Sn随n的增大而增大,而S1≤Sn<2,
,所以Sn随n的增大而增大,而S1≤Sn<2,此时Sn有最小值为1,但无最大值.-------------------------------(3分)
(只给出答案而不能够说明理由的,得1分)
当
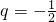 时,
时,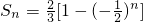
若n=2k,k∈N*时,
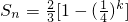 ,所以Sn随k的增大而增大,
,所以Sn随k的增大而增大,即n是偶数时,
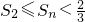 ,即
,即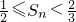
若n=2k-1,k∈N*时,
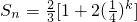 ,所以Sn随k的增大而减小,
,所以Sn随k的增大而减小,即n是奇数时,
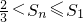 ,即
,即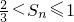
所以
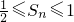 ,Sn有最大值为1,最小值为
,Sn有最大值为1,最小值为 .---(4分)
.---(4分)(只给出答案而不能够说明理由的,得1分)
(3)
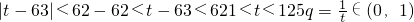 .
.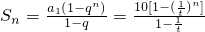 且Sn随着n的增大而增大
且Sn随着n的增大而增大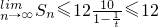 -----------------------(3分)
-----------------------(3分)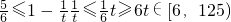 -----------------------------(2分)
-----------------------------(2分)t∈N*?124-6+1=119个.----------------------------------------(1分)
分析:(1)利用等比数列的求和公式,进而可求
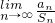 的值;
的值;(2)当
 时,
时,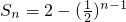 ,所以Sn随n的增大而增大,而S1≤Sn<2,此时Sn有最小值为1,但无最大值当
,所以Sn随n的增大而增大,而S1≤Sn<2,此时Sn有最小值为1,但无最大值当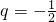 时,
时,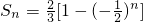 ,分n是偶数,奇数讨论求最大值与最小值
,分n是偶数,奇数讨论求最大值与最小值(3)根据t满足不等式|t-63|<62,可确定q的范围,进而可得Sn随着n的增大而增大,利用9<Sn<12,可求解.
点评:本题以等比数列为载体,考查数列的极限,考查等比数列的求和,考查数列的单调性,属于中档题.

练习册系列答案
相关题目