题目内容
半径为5的圆过点A（-2，6），且以M（5，4）为中点的弦长为2| 5 |
分析：设圆的方程是（x-a）2+（y-b）2=25，由（-2，6）在圆上，及弦长公式得到方程组，解方程组求得
a，b 的值，即得圆的方程．
a，b 的值，即得圆的方程．
解答：解：设圆心坐标为P（a，b），则圆的方程是（x-a）2+（y-b）2=25，
∵（-2，6）在圆上，∴（a+2）2+（b-6）2=25，又以M（5，4）为中点的弦长为2
，
∴|PM|2=r2-
2，即（a-5）2+（b-4）2=20，
联立方程组
，两式相减得7a-2b=3，将b=
代入
得53a2-194a+141=0，解得a=1或a=
，相应的求得b1=2，b2=
，
∴圆的方程是（x-1）2+（y-2）2=25，或（x-
）2+（y-
）2=25．
∵（-2，6）在圆上，∴（a+2）2+（b-6）2=25，又以M（5，4）为中点的弦长为2
| 5 |
∴|PM|2=r2-
| 5 |
联立方程组
|
| 7a-3 |
| 2 |
得53a2-194a+141=0，解得a=1或a=
| 141 |
| 53 |
| 414 |
| 53 |
∴圆的方程是（x-1）2+（y-2）2=25，或（x-
| 141 |
| 53 |
| 414 |
| 53 |
点评：本题考查用待定系数法求圆的标准方程，以及弦长公式的应用．
练习册系列答案
相关题目
，求此圆的方程。 
,求此圆的方程.
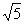，求此圆的方程。