题目内容
某同学探究函数f(x)=x+
(x>0)的最小值,并确定相应的x的值.先列表如下:
请观察表中y值随x值变化的特点,完成下列问题:((1)(2)问的填空只要写出结果即可)
(1)若x1x2=4,则 f(x1)
(x>0)在区间 (0,2)上递减,则f(x)在区间
(2)当x=
(x>0)的最小值为
(3)根据函数f(x)的有关性质,你能得到函数f(x)=x+
(x<0)的最大值吗?为什么?
| 4 |
| x |
| x | … |
|
|
1 |
|
2 |
|
4 | 8 | 16 | … | ||||||||
| y | … | 16.25 | 8.5 | 5 |
|
4 |
|
5 | 8.5 | 16.25 | … |
(1)若x1x2=4,则 f(x1)
=
=
f(x2).(请填写“>,=,<”号);若函数f(x)=x+| 4 |
| x |
(2,+∞)
(2,+∞)
上递增;(2)当x=
2
2
时,f(x)=x+| 4 |
| x |
4
4
;(3)根据函数f(x)的有关性质,你能得到函数f(x)=x+
| 4 |
| x |
分析:(1)根据表格和函数单调性的定义,直接写出;
(2)根据表格中的数据写出;
(3)先求出f(x)=x+
的定义域,再验证f(-x)=-f(x),判断出函数是奇函数,得到图象关于原点对称,再求出当x<0时的函数的最大值.
(2)根据表格中的数据写出;
(3)先求出f(x)=x+
| 4 |
| x |
解答:解:(1)=,(2,+∞) (左端点可以闭),
(2)由表格得,x=2时,f(x)=x+
(x>0)取最小值是4
(3)∵函数 f(x)=x+
的定义域是{x|x≠0},且f(-x)=-f(x),
∴f(x)=x+
是奇函数,
∴函数f(x)=x+
(x<0)与函数f(x)=x+
(x>0)关于原点对称,
则函数f(x)=x+
(x<0)在x=-2时取得最大值-4. …
(2)由表格得,x=2时,f(x)=x+
| 4 |
| x |
(3)∵函数 f(x)=x+
| 4 |
| x |
∴f(x)=x+
| 4 |
| x |
∴函数f(x)=x+
| 4 |
| x |
| 4 |
| x |
则函数f(x)=x+
| 4 |
| x |
点评:本题考查了函数的单调性与奇偶性的综合应用,以及观察能力,难度不大.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
某同学探究函数 (x>0)的最小值,并确定相应的x的值.先列表如下:
(x>0)的最小值,并确定相应的x的值.先列表如下:
| x | … |  |  | 1 |  | 2 |  | 4 | 8 | 16 | … |
| y | … | 16.25 | 8.5 | 5 |  | 4 |  | 5 | 8.5 | 16.25 | … |
请观察表中y值随x值变化的特点,完成下列问题:((1)(2)问的填空只要写出结果即可)
(1)若x1x2=4,则 f(x1)______f(x2).(请填写“>,=,<”号);若函数 (x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;
(x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;
(2)当x=______时, (x>0)的最小值为______;
(x>0)的最小值为______;
(3)根据函数f(x)的有关性质,你能得到函数 (x<0)的最大值吗?为什么?
(x<0)的最大值吗?为什么?
某同学探究函数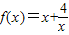 (x>0)的最小值,并确定相应的x的值.先列表如下:
(x>0)的最小值,并确定相应的x的值.先列表如下:
请观察表中y值随x值变化的特点,完成下列问题:((1)(2)问的填空只要写出结果即可)
(1)若x1x2=4,则 f(x1)______f(x2).(请填写“>,=,<”号);若函数 (x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;
(x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;
(2)当x=______时,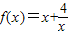 (x>0)的最小值为______;
(x>0)的最小值为______;
(3)根据函数f(x)的有关性质,你能得到函数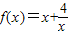 (x<0)的最大值吗?为什么?
(x<0)的最大值吗?为什么?
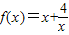 (x>0)的最小值,并确定相应的x的值.先列表如下:
(x>0)的最小值,并确定相应的x的值.先列表如下:| x | … |  |  | 1 |  | 2 |  | 4 | 8 | 16 | … |
| y | … | 16.25 | 8.5 | 5 | 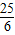 | 4 | 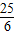 | 5 | 8.5 | 16.25 | … |
(1)若x1x2=4,则 f(x1)______f(x2).(请填写“>,=,<”号);若函数
 (x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;
(x>0)在区间 (0,2)上递减,则f(x)在区间______ 上递增;(2)当x=______时,
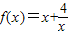 (x>0)的最小值为______;
(x>0)的最小值为______;(3)根据函数f(x)的有关性质,你能得到函数
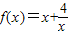 (x<0)的最大值吗?为什么?
(x<0)的最大值吗?为什么?