题目内容
某同学探究函数f(x)=x+
（x＞0）的最小值，并确定相应的x的值．先列表如下：
请观察表中y值随x值变化的特点，完成下列问题：（（1）（2）问的填空只要写出结果即可）
（1）若x1x2=4，则 f（x1）______f（x2）．（请填写“＞，=，＜”号）；若函数f(x)=x+
（x＞0）在区间 （0，2）上递减，则f（x）在区间______ 上递增；
（2）当x=______时，f(x)=x+
（x＞0）的最小值为______；
（3）根据函数f（x）的有关性质，你能得到函数f(x)=x+
（x＜0）的最大值吗？为什么？
| 4 |
| x |
| x | … |
|
|
1 |
|
2 |
|
4 | 8 | 16 | … | ||||||||
| y | … | 16.25 | 8.5 | 5 |
|
4 |
|
5 | 8.5 | 16.25 | … |
（1）若x1x2=4，则 f（x1）______f（x2）．（请填写“＞，=，＜”号）；若函数f(x)=x+
| 4 |
| x |
（2）当x=______时，f(x)=x+
| 4 |
| x |
（3）根据函数f（x）的有关性质，你能得到函数f(x)=x+
| 4 |
| x |
（1）=，（2，+∞） （左端点可以闭），
（2）由表格得，x=2时，f(x)=x+
（x＞0）取最小值是4
（3）∵函数 f(x)=x+
的定义域是{x|x≠0}，且f（-x）=-f（x），
∴f(x)=x+
是奇函数，
∴函数f(x)=x+
（x＜0）与函数f(x)=x+
（x＞0）关于原点对称，
则函数f(x)=x+
（x＜0）在x=-2时取得最大值-4． …
（2）由表格得，x=2时，f(x)=x+
| 4 |
| x |
（3）∵函数 f(x)=x+
| 4 |
| x |
∴f(x)=x+
| 4 |
| x |
∴函数f(x)=x+
| 4 |
| x |
| 4 |
| x |
则函数f(x)=x+
| 4 |
| x |
练习册系列答案
相关题目
某同学探究函数
（x＞0）的最小值，并确定相应的x的值．先列表如下：
| x | … |  |  | 1 |  | 2 |  | 4 | 8 | 16 | … |
| y | … | 16.25 | 8.5 | 5 |  | 4 | | 5 | 8.5 | 16.25 | … |
请观察表中y值随x值变化的特点，完成下列问题：（（1）（2）问的填空只要写出结果即可）
（1）若x1x2=4，则 f（x1）______f（x2）．（请填写“＞，=，＜”号）；若函数（x＞0）在区间 （0，2）上递减，则f（x）在区间______ 上递增；
（2）当x=______时，（x＞0）的最小值为______；
（3）根据函数f（x）的有关性质，你能得到函数（x＜0）的最大值吗？为什么？
某同学探究函数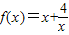
（x＞0）的最小值，并确定相应的x的值．先列表如下：
请观察表中y值随x值变化的特点，完成下列问题：（（1）（2）问的填空只要写出结果即可）
（1）若x1x2=4，则 f（x1）______f（x2）．（请填写“＞，=，＜”号）；若函数
（x＞0）在区间 （0，2）上递减，则f（x）在区间______ 上递增；
（2）当x=______时，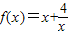
（x＞0）的最小值为______；
（3）根据函数f（x）的有关性质，你能得到函数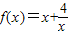
（x＜0）的最大值吗？为什么？
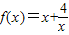（x＞0）的最小值，并确定相应的x的值．先列表如下：| x | … |  |  | 1 |  | 2 |  | 4 | 8 | 16 | … |
| y | … | 16.25 | 8.5 | 5 | 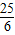 | 4 | 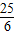 | 5 | 8.5 | 16.25 | … |
（1）若x1x2=4，则 f（x1）______f（x2）．（请填写“＞，=，＜”号）；若函数
（x＞0）在区间 （0，2）上递减，则f（x）在区间______ 上递增；（2）当x=______时，
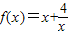（x＞0）的最小值为______；（3）根据函数f（x）的有关性质，你能得到函数
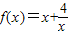（x＜0）的最大值吗？为什么？