题目内容
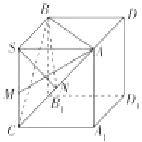
【题目】在正三棱锥S﹣ABC中，AB= 
，M是SC的中点，AM⊥SB，则正三棱锥S﹣ABC外接球的球心到平面ABC的距离为 ．
【答案】
【解析】解：取AC的中点N，连接BN，因为SA=SC，所以AC⊥SN，由∵△ABC是正三角形，∴AC⊥BN． 故AC⊥平面SBN，AC⊥BC．
又∵AM⊥SB，AC∩AM=A，∴SB⊥平面SAC，SB⊥SA且SB⊥SC
故得到SB，SA，SC是三条两两垂直的．可以看成是一个正方体切下来的一个正三棱锥．
故外接圆直径2R= 
∵AB= 
，∴SA=1．
那么：外接球的球心与平面ABC的距离为正方体对角线的 
，即d= ．
所以答案是： ．
【考点精析】利用棱锥的结构特征对题目进行判断即可得到答案，需要熟知侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方．
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了调查每天人们使用手机的时间，我校某课外兴趣小组在天府广场随机采访男性、女性用户各50 名，其中每天玩手机超过6小时的用户列为“手机控”，否则称其为“非手机控”，调查结果如下：
手机控 | 非手机控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
（1）根据以上数据，能否有60%的把握认为“手机控”与“性别”有关？
（2）现从调查的女性用户中按分层抽样的方法选出5人，求所抽取5人中“手机控”和“非手机控”的人数；
（3）从（2）中抽取的5人中再随机抽取3人，记这3人中“手机控”的人数为X，试求X的分布列与数学期望． 参考公式： 
．
参考数据：
P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.456[ | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
