题目内容

3．曲线y=ex+3在（0，4）处的切线方程为（　　）
A．2x+y-4=0B．2x-y+4=0C．x-y+4=0D．x+y-4=0

分析 求出函数的导数，求得切线的斜率，由点斜式方程可得切线的方程．

解答 解：y=ex+3的导数为y′=ex，
即有曲线y=ex+3在（0，4）处的切线斜率为k=1，
即有曲线y=ex+3在（0，4）处的切线方程为y-4=x，
即为x-y+4=0，
故选C．

点评 本题考查导数的运用：求切线方程，主要考查导数的几何意义：函数在某点处的导数即为曲线在该点处的切线的斜率，正确求导和运用点斜式方程是解题的关键．

练习册系列答案
相关题目
13．已知函数f（x）=$\frac{1}{3}$x2-ax+4（a＞0）；
（1）求函数f（x）的单调区间及极值；
（2）当x∈[-3，3]时，函数y=f（x）的图象上任意一点的切线斜率恒小于1，求实数a的取值范围．
14．若方程x2-2kx+k2-1=0有两个不等实数根介于-2与4之间，求k的范围．
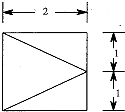11．已知四棱锥，它的底面是边长为2的正方形，其俯视图如图所示，侧视图为直角三角形，则该四棱锥的侧面中直角三角形的个数有3个，该四棱锥的体积为$\frac{4}{3}$．
18．如图，已知PE切圆O于点E，割线PBA交圆O于A，B两点，∠APE的平分线和AE，BE分别交于点C，D．
（1）求证：CE=DE；
（2）求证：$\frac{PE}{PA}=\frac{CE}{CA}$．
8．如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是（　　）
A．AC⊥SB
B．AB∥平面SCD
C．AC⊥面SBD
D．AB与SC所成的角等于DC与SA所成的角
15．编号为1、2、3、4的四封信本应分别投入编号为①、②、③、④的四个邮箱，通过邮递员投递，可能出现信件错投若有序数组（a1，a2，a3，a4）是四个邮箱依序实际收到的信件编号，且有序数组为1、2、3、4的排列，共有24种情况．用X=|a1-1|+|a2-2|+|a3-3|+|a4-4|表示信件编号与邮箱编号的偏离程度．
（1）写出X的可能性集合（不必说明原因），并列出X=2的全部有序数组；
（2）若规定：X取最小值时，为“好评”；X取最大值时，为“差评”；X取其他值时，为“一般”．试求邮递员被评为“一般”的概率．
12．已知直线l的参数方程$\left\{\begin{array}{l}{x=-1-\frac{\sqrt{3}}{2}t}\\{y=\sqrt{3}+\frac{1}{2}t}\end{array}\right.$ （t为参数），⊙L的极坐标方程为ρ=4sin（θ-$\frac{π}{2}$），求直线l的普通方程和⊙L的直角坐标方程．
13．已知函数f（x）=x-$\frac{a}{x}$．g（x）=2ln（x+m），
（Ⅰ）当m=0时，存在x0∈[$\frac{1}{e}$，e]（e为自然对数的底数），使x0f（x0）≥g（x0），求实数a的取值范围；
（Ⅱ）当a=m=1时，
（1）求最大正整数n，使得对任意n+1个实数xi（i=1，2…，n+1），当xi∈[e-1，2]（e为自然对数的底数）时，都有$\sum_{i=1}^{n}$f（xi）＜2015g（xn+1）成立；
（2）设H（x）=xf（x）+g（x），在H（x）的图象上是否存在不同的两点A（x1，y1），B（x2，y2）（x1＞x2＞-1），使得H（x1）-H（x2）=H′（$\frac{{x}_{1}+{x}_{2}}{2}$）（x1-x2）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网