题目内容
20．下列说法中正确的有（1）命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠l，则x2-3x+2≠0”；
（2）“x＞2”是“x2-3x+2＞0”的充分不必要条件；
（3）对于命题p：?x∈R，x2+x+1＜0，则￢p：?x∈R，x2+x+1≥0
（4）若P∧q为假命题，则P、q均为假命题．（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 （1）由逆否命题的意义即可判断出正误；
（2）由x2-3x+2＞0解得x＞2或x＜1，即可判断出结论；
（3）由￢p的定义即可判断出正误；
（4）若P∧q为假命题，则P、q至少有一个为假命题，即可判断出正误．
解答 解：（1）命题“若x2-3x+2=0，则x=1”，由逆否命题的意义可得：其逆否命题为“若x≠l，则x2-3x+2≠0”，正确；
（2）由x2-3x+2＞0解得x＞2或x＜1，∴“x＞2”是“x2-3x+2＞0”的充分不必要条件，正确；
（3）对于命题p：?x∈R，x2+x+1＜0，由￢p的定义可知￢p：?x∈R，x2+x+1≥0，正确；
（4）若P∧q为假命题，则P、q至少有一个为假命题，因此不正确．
综上可得：正确命题的个数为3．
故选：C．
点评 本题考查了简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
10．设函数f（x）=ex（2x-1）+ax-a，其中a＞-1，若关于x不等式f（x）＜0的整数解有且只有一个，则实数a的取值范围为（ ）
| A． | （-1，$\frac{3}{2e}$] | B． | （-$\frac{3}{4}$，$\frac{3}{2e}$] | C． | （-$\frac{3}{4}$，-$\frac{3}{2e}$] | D． | （-1，-$\frac{3}{2e}$] |
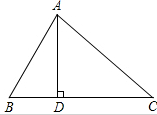如图，在△ABC中，AD⊥BC，$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$，BD=4，CD=6．