题目内容
1.已知函数f(x)是奇函数,当x<0,f(x)=-x2+x.若不等式f(x)-x≤2logax(a>0,a≠1)对?x∈(0,$\frac{\sqrt{2}}{2}$]恒成立,则实数a的取值范围是[$\frac{1}{4}$,1).分析 先求出f(x)在x>0的解析式,不等式f(x)-x≤2logax(a>0,a≠1)对?x∈(0,$\frac{\sqrt{2}}{2}$]恒成立,转化为loga$\sqrt{a}$≤loga$\frac{1}{2}$,分类讨论即可.
解答 解:函数f(x)是奇函数,当x<0,f(x)=-x2+x
∴f(-x)=-f(x),
设x>0,则-x<0,
∴f(-x)=-x2-x,
∴f(x)=x2+x,
∵不等式f(x)-x≤2logax(a>0,a≠1)对?x∈(0,$\frac{\sqrt{2}}{2}$]恒成立,
∴x2+x-x≤2logax(a>0,a≠1)对?x∈(0,$\frac{\sqrt{2}}{2}$]恒成立,
∴x2≤logax2,
∴($\frac{\sqrt{2}}{2}$)2≤loga($\frac{\sqrt{2}}{2}$)2,
∴loga$\sqrt{a}$=$\frac{1}{2}$≤loga$\frac{1}{2}$,
当a>1时,$\sqrt{a}$≤$\frac{1}{2}$,解得a≤$\frac{1}{4}$,此时无解,
当0<a<1时,$\sqrt{a}$≥$\frac{1}{2}$,解得a≥$\frac{1}{4}$,此时$\frac{1}{4}$≤a<1,
综上所述a的取值范围为[$\frac{1}{4}$,1).
故答案为:[$\frac{1}{4}$,1).
点评 本题是恒成立问题,通过研究函数的单调性,借助于最值求出参数的范围.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
11.若ab>0,则直线ax+by=0倾斜角α的取值范围是( )
| A. | 0°<α<90° | B. | 90°<α<180° | C. | 0°<α<180° | D. | 45°<α<90° |
12.下列函数中,周期为2的奇函数为( )
| A. | y=sin2x | B. | y=cos2πx | C. | y=cos[2(πx-$\frac{π}{4}$)]-$\frac{1}{2}$ | D. | y=tan$\frac{π}{2}$x |
6.设随机变量X1,…,Xn独立同分布,Xi~N(μ,σ2)(1≤i≤n),则$\overline{X}$=$\frac{1}{n}$$\sum_{i=1}^{n}$Xi~( )
| A. | N(μ,σ2) | B. | N(0,1) | C. | N(μ,$\frac{{σ}^{2}}{n}$) | D. | N(1,1) |
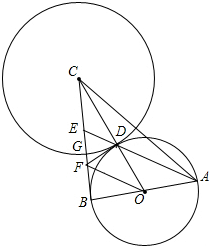 如图:Rt△ABC中,∠ABC=90°,AB=BC.以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连OF.⊙C切⊙O于点D,交BC于G.
如图:Rt△ABC中,∠ABC=90°,AB=BC.以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连OF.⊙C切⊙O于点D,交BC于G.