题目内容
对 ,定义
,定义 ,则函数
,则函数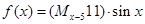 是( )
是( )
| A.奇函数但非偶函数; | B.偶函数但非奇函数; |
| C.既是奇函数又是偶函数; | D.非奇非偶函数 |
B
解析试题分析:根据定义得: ,因为定义域 R关于原点对称,又
,因为定义域 R关于原点对称,又 ,所以偶函数但非奇函数。
,所以偶函数但非奇函数。
考点:函数奇偶性的判断。
点评:本题给出新定义,然后根据新定义写出新函数,判断新函数的奇偶性。考查了学生的理解能力,同时也考查了函数的奇偶性的判断方法,属于中档题。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知二次函数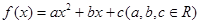 ,满足:对任意实数
,满足:对任意实数 ,都有
,都有 ,且当
,且当 时,有
时,有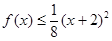 成立,又
成立,又 ,则
,则 为( )
为( )
| A.1 | B. | C.2 | D.0 |
已知 ,若方程
,若方程 存在三个不等的实根
存在三个不等的实根 ,则
,则 的取值范围是
的取值范围是
A. | B. | C. | D.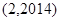 |
函数y=(2k+1)x+b在(-∞,+∞)上是减函数,则( )
A.k> | B.k< | C.k> | D.k< |
 的零点个数是( )
的零点个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
已知函数 ,且
,且 .则( )
.则( )
A. | B. |
C. | D. |
函数 的实数解落在的区间是( )
的实数解落在的区间是( )
A. | B.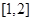 | C. | D. |
数 的定义域是( )
的定义域是( )
A. | B. | C. | D. |
若 ,则满足不等式
,则满足不等式 的x的范围是( )
的x的范围是( )
A.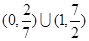 | B.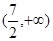 |
C. | D. |