题目内容
数
的定义域是（ ）
A． | B． | C． | D． |
D
解析试题分析：由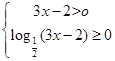
得：
，所以函数的定义域为。
考点：函数的定义域。
点评：求函数的定义域需要从以下几个方面入手： （1）分母不为零 ；（2）偶次根式的被开方数非负；（3）对数中的真数部分大于0； （4）指数、对数的底数大于0，且不等于1 ； （5）y=tanx中x≠kπ+π/2；y=cotx中x≠kπ等； ( 6 )
中
。
练习册系列答案
名校通行证有效作业系列答案
相关题目
二次函数
的图象的对称轴为
，则当
时，
的值为（ ）
A． | B．1 | C．17 | D．25 |
对
，定义
，则函数
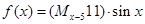是（ ）
| A．奇函数但非偶函数； | B．偶函数但非奇函数； |
| C．既是奇函数又是偶函数； | D．非奇非偶函数 |
函数f（x）=4x－3·2x＋3的值域为[1，7]，则f（x）的定义域为（ ）
| A．（－1，1）∪[2，4] ( | B．（0，1）∪[2，4] |
| C． [2，4] | D．（－∞，0] ∪[1，2] |
函数
的零点所在的大致区间是（ ）
A． | B． | C． 和 | D． |
若
，则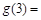
（ ）
A． | B． | C． | D． |
已知定义在R上的奇函数
，满足
,且在区间[0,2]上是减函数,则（ ）
A． | B． |
C． | D． |
幂指函数
在求导时，可运用对数法：在函数解析式两边求对数得
，两边同时求导得
，于是
。运用此方法可以探求得知
的一个单调递增区间为（ ）
| A．(0,2) | B．(2,3) | C．(e,4) | D．(3,8) |
方程
的根的个数是（ ）
| A．0个 | B．1个 | C．2个 | D．3个 |