题目内容

（2008•徐汇区二模）设F1(-
3
，0)，F2(
3
，0)，若动点P（x，y）满足|
PF1
|+|
PF2
|=4．
（1）求动点P的轨迹方程；（2）求
PF1
•
PF2
的最大值和最小值．
分析：（1）由于点P满足|PF1|+|PF2|为常数，且大于线段|F1F2|的长，P的轨迹是椭圆，再根据椭圆的标准方程求解动点P的轨迹方程；
（2）由
PF1
•
PF2
=x2+y2-3=
1
4
(3x2-8)，写出其定义域，利用函数思想求最大值和最小值即可．
解答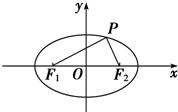：解：（1）由椭圆定义易得动点P的轨迹方程为
x2
4
+y2=1；------（6分）
（2）由
PF1
•
PF2
=x2+y2-3=
1
4
(3x2-8)，
∵x∈[-2，2]-----------（10分）
故当x=0时，即点P为椭圆短轴端点时，
PF1
•
PF2
有最小值-2----（12分）
当x=±2，即点P为椭圆长轴端点时，
PF1
•
PF2
有最大值1．--------（14分）
点评：本题主要了向量在几何中的应用、椭圆的定义．点P满足|PF1|+|PF2|=|F1F2|，P的轨迹是线段F1F2；点P满足|PF1|+|PF2|为常数，且大于线段|F1F2|的长，P的轨迹是椭圆；小于线段|F1F2|的长，P点无轨迹．
练习册系列答案
相关题目
（2008•徐汇区二模）已知整数对的数列如下：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），（1，5），（2，4），…，则第24个数对是
（3，5）
（3，5）
．
（2008•徐汇区二模）（1-i）2•i=
2
2
．
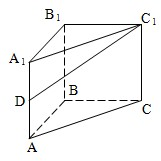（2008•徐汇区二模）如图直三棱柱ABC-A1B1C1的侧棱长为2，底面△ABC是等腰直角三角形，∠ABC=90°，AC=2，D是AA1的中点
（1）求三棱柱ABC-A1B1C1的体积V；
（2）求C1D与上底面所成角的大小．（用反三角表示）
（2008•徐汇区二模）设集合M={（x，y）|x2-y2=1，x∈R，y∈R}N={(x，y)|y=
x2
+1，x∈R，y∈R}，则集合M∩N中元素的个数为
2
2
．
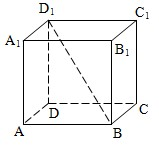（2008•徐汇区二模）正方体ABCD-A1B1C1D1中，异面直线BD1与AA1所成的角的大小是
arctg
2
arctg
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网