题目内容

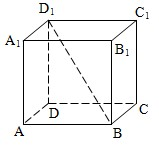（2008•徐汇区二模）正方体ABCD-A1B1C1D1中，异面直线BD1与AA1所成的角的大小是
arctg
2
arctg
2
．
分析：设正方体的棱长为1，由正方体的性质可得∠D1BB1 即为AA1和BD1所成的角，Rt△D1BB1中，根据
解答：解：设正方体的棱长为1，则∠D1BB1 即为AA1和BD1所成的角．
在Rt△D1BB1中，tan∠D1BB1=
D1B1
BB 1
=
2
1
=
2
．
即AA1和BD1所成的角的正切值为
2
，
故异面直线BD1与AA1所成的角的大小arctan
2
．
故答案为：arctan
2
．
点评：本题考查异面直线所成的角的定义和求法，直线和平面平行的判定方法，利用正方体的性质是解题的关键．
练习册系列答案
相关题目
（2008•徐汇区二模）已知整数对的数列如下：（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），（1，5），（2，4），…，则第24个数对是
（3，5）
（3，5）
．
（2008•徐汇区二模）（1-i）2•i=
2
2
．
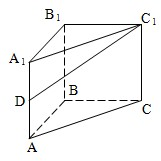（2008•徐汇区二模）如图直三棱柱ABC-A1B1C1的侧棱长为2，底面△ABC是等腰直角三角形，∠ABC=90°，AC=2，D是AA1的中点
（1）求三棱柱ABC-A1B1C1的体积V；
（2）求C1D与上底面所成角的大小．（用反三角表示）
（2008•徐汇区二模）设集合M={（x，y）|x2-y2=1，x∈R，y∈R}N={(x，y)|y=
x2
+1，x∈R，y∈R}，则集合M∩N中元素的个数为
2
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网