题目内容
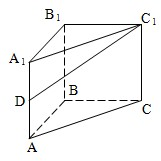 (2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点
(2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点(1)求三棱柱ABC-A1B1C1的体积V;
(2)求C1D与上底面所成角的大小.(用反三角表示)
分析:(1)利用三棱柱ABC-A1B1C1的体积公式,关键是求底面积,而底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,故易求;
(2)由于是直三棱柱,故C1D与上底面所成角即为∠DC1A1,从而利用正切函数可求.
(2)由于是直三棱柱,故C1D与上底面所成角即为∠DC1A1,从而利用正切函数可求.
解答:(1)解:由已知条件,,∠ABC=90°,AC=2,易得AB=BC=
,
所以V=
•2•
•
=2------------------------------------------------------------------------(5分)
(2)解:C1D与上底面所成角即为∠DC1A1,----------------------------------------------(7分)
由DA1=1,A1C1=2得tan∠DC1A1=
,
所以C1D与上底面所成角的大小为arctan
-----------------------------------------------(12分)
| 2 |
所以V=
| 1 |
| 2 |
| 2 |
| 2 |
(2)解:C1D与上底面所成角即为∠DC1A1,----------------------------------------------(7分)
由DA1=1,A1C1=2得tan∠DC1A1=
| 1 |
| 2 |
所以C1D与上底面所成角的大小为arctan
| 1 |
| 2 |
点评:本题的考点是直线与平面所成的角,主要考查线面角,关键是利用几何体寻找线面角,考查几何体体积公式的运用.

练习册系列答案
相关题目
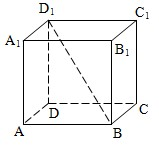 (2008•徐汇区二模)正方体ABCD-A1B1C1D1中,异面直线BD1与AA1所成的角的大小是
(2008•徐汇区二模)正方体ABCD-A1B1C1D1中,异面直线BD1与AA1所成的角的大小是