题目内容
(2008•徐汇区二模)设集合M={(x,y)|x2-y2=1,x∈R,y∈R}N={(x,y)|y=
+1,x∈R,y∈R},则集合M∩N中元素的个数为
| x | 2 |
2
2
.分析:由于集合M,N表示点集,故集合M∩N中元素的个数,可转换为直线与曲线的交点的个数,通过联立方程组成方程组,考查方程足足解的个数即可解决.
解答:解:联立集合M,N中的方程得
,∴有3x2-4x-8=0
∵△>0,∴方程有两个不等的实数根
∴集合M∩N中元素的个数为2
故答案为2
|
∵△>0,∴方程有两个不等的实数根
∴集合M∩N中元素的个数为2
故答案为2
点评:本题的考点是直线与圆锥曲线的位置关系,考查直线与曲线的交点的个数,关键是理解交集的含义,将问题合理等价转换,属于中档题,也是高考常会考的题型.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
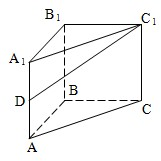 (2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点
(2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点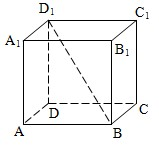 (2008•徐汇区二模)正方体ABCD-A1B1C1D1中,异面直线BD1与AA1所成的角的大小是
(2008•徐汇区二模)正方体ABCD-A1B1C1D1中,异面直线BD1与AA1所成的角的大小是