题目内容
 如图,在正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,P为AD上一动点,记α为异面直线PM与D1N所成的角,则α的集合是( )
如图,在正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,P为AD上一动点,记α为异面直线PM与D1N所成的角,则α的集合是( )A、{
| ||||
B、{α|
| ||||
C、{α|
| ||||
D、{α|
|
考点:集合的表示法
专题:
分析:根据已知条件建立空间直角坐标系,求出向量
,
的坐标,求这两向量夹角即可.
| PM |
| D1N |
解答:解:如图,分别以边DA,DC,DD1所在直线为x轴,y轴,z轴,建立如图所示空间直角坐标系,设正方体边长
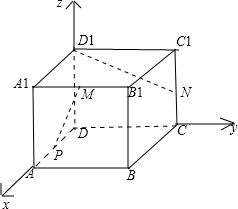 为1,P(x,0,0)(0≤x≤1),并能确定以下几点坐标:
为1,P(x,0,0)(0≤x≤1),并能确定以下几点坐标:
M(1,
,1),D1(0,0,1),N(0,1,
);
∴
=(1-x,
,1),
=(0,1,-
);
∴
•
=0;
∴
⊥
,∴α=
.
故选A.
 为1,P(x,0,0)(0≤x≤1),并能确定以下几点坐标:
为1,P(x,0,0)(0≤x≤1),并能确定以下几点坐标:M(1,
| 1 |
| 2 |
| 1 |
| 2 |
∴
| PM |
| 1 |
| 2 |
| D1N |
| 1 |
| 2 |
∴
| PM |
| D1N |
∴
| PM |
| D1N |
| π |
| 2 |
故选A.
点评:考查异面直线所成角,以及通过建立空间直角坐标系,用向量求异面直线所成角的方法,两非零向量垂直的充要条件..

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
设集合A={1,2,3},B={1,2,9},x∈A且x∉B,则x=( )
| A、1 | B、2 | C、3 | D、9 |
定义A×B={z|z=xy,x∈A且y∈B},若A={x|-1<x<2},B={-1,2},则A×B=( )
| A、{x|-1<x<2} | B、{-1,2} | C、{x|-2<x<2} | D、{x|-2<x<4} |
设集合A={x|-x2-4x+5>0},则A=( )
| A、{x|-5<x<1} | B、{x|x<-5或x>1} | C、{x|-1<x<5} | D、{x|x<-1或x>5} |
已知不等式{x|ax-2>0}的解集为{x|x<-4},则a的值为( )
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
设全集为R,集合A={x|x<1},B={x|
>0},则( )
| 1 |
| x-2 |
| A、(∁RA)⊆B |
| B、A⊆(∁RB) |
| C、A⊆B |
| D、B⊆A |
 (
( )任意排成
)任意排成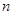 行
行 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.若
,称这些比值中的最小值为这个数表的“特征值”.若 表示某个
表示某个 行第
行第 列的数(
列的数( ,
, ),且满足
),且满足 ,当
,当 时数表的“特征值”为_________
时数表的“特征值”为_________ ,B=
,B= ,求矩阵A-1B.
,求矩阵A-1B.