Question

【题目】已知双曲线 ﹣ =1（a＞0，b＞0）的左、右焦点分别为F1、F2 ， 点P（x0 ， ）为双曲线上一点，若△PF1F2的内切圆半径为1，且圆心G到原点O的距离为 ，则双曲线的离心率是 ．

Answer 1

【答案】
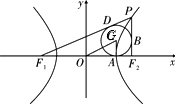
【解析】解：设P为第一象限的点，

圆与F1F2，PF1，PF2的切点分别为A'，B，D．

∵|PF1|﹣|PF2|=2a，|PD|=|PB|，|DF1|=|A'F1|，|BF2|=|A'F2|，

即为|PD|+|DF1|﹣|PB|﹣|BF2|=|DF1|﹣|BF2|=|A'F1|﹣|A'F2|=2a，

且|A'F1|+|A'F2|=2c，可得|A'F2|=c﹣a，

则A与A'重合，则|OA'|=|OA|=a，

故 = ，即a=2．

又△PF1F2的面积S= × ×|2c|= （|F1F2|+|PF1|+|PF2|）×1，

∴|PF1|+|PF2|=3c，

∵|PF1|﹣|PF2|=2a，

∴|PF1|= ，|PF2|= ，

∵|PF1|= ，|PF2|= ，联立化简得x0=3．

P代入双曲线方程，联立解得b= ，c= =3，

即有双曲线的离心率为e= = ．

所以答案是： ．