题目内容
直线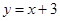 与曲线
与曲线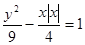 的交点的个数是 个.
的交点的个数是 个.
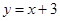 与曲线
与曲线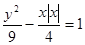 的交点的个数是 个.
的交点的个数是 个.3
试题分析:当

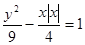 等价于
等价于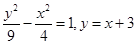 代入可知5x=24,可知交点个数为1个,当
代入可知5x=24,可知交点个数为1个,当
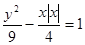 等价于
等价于 代入可知
代入可知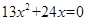 ,则可知满足交点的个数有2个,那么综上可知,交点个数一共有3个,答案为3.
,则可知满足交点的个数有2个,那么综上可知,交点个数一共有3个,答案为3.点评:此题考查了此题考查了直线与椭圆,双曲线的位置关系,做题时应认真审题,找出内在联系,做题时应认真审题,找出内在联系

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
题目内容
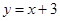 与曲线
与曲线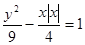 的交点的个数是 个.
的交点的个数是 个.
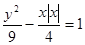 等价于
等价于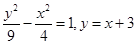 代入可知5x=24,可知交点个数为1个,当
代入可知5x=24,可知交点个数为1个,当
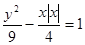 等价于
等价于 代入可知
代入可知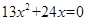 ,则可知满足交点的个数有2个,那么综上可知,交点个数一共有3个,答案为3.
,则可知满足交点的个数有2个,那么综上可知,交点个数一共有3个,答案为3.
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案