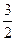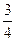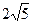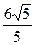题目内容
已知圆C经过点A(1,-1),B(-2,0),C(
,1)直线l:mx-y+1-m=0
(1)求圆C的方程;
(2)求证:?m∈R,直线l与圆C总有两个不同的交点;
(3)若直线l与圆C交于M、N两点,当|MN|=
时,求m的值.
| 5 |
(1)求圆C的方程;
(2)求证:?m∈R,直线l与圆C总有两个不同的交点;
(3)若直线l与圆C交于M、N两点,当|MN|=
| 17 |
(1)设圆的方程为x2+y2+Dx+Ey+F=0
∵A(1,-1),B(-2,0),C(
,1)在圆上
∴
,解之得
因此,圆的方程为x2+y2-2y-4=0;…(4分)
(2)将圆化成标准方程,得x2+(y-1)2=5
∴圆心是(0,1),半径为r=
∵直线l:mx-y+1-m=0恒过点P(1,1),
而P点满足:12+(1-1)2<5,说明点P在圆内
∴?m∈R,直线l与圆C总有两个不同的交点;…(8分)
(3)∵圆心(0,1),半径为r=
,
∴圆心到直线l的距离d=
=
又∵|MN|=2
∴
=2
,解之得m=
或-
.…(12分)
∵A(1,-1),B(-2,0),C(
| 5 |
∴
|
|
因此,圆的方程为x2+y2-2y-4=0;…(4分)
(2)将圆化成标准方程,得x2+(y-1)2=5
∴圆心是(0,1),半径为r=
| 5 |
∵直线l:mx-y+1-m=0恒过点P(1,1),
而P点满足:12+(1-1)2<5,说明点P在圆内
∴?m∈R,直线l与圆C总有两个不同的交点;…(8分)
(3)∵圆心(0,1),半径为r=
| 5 |
∴圆心到直线l的距离d=
| |-m| | ||
|
| |m| | ||
|
又∵|MN|=2
| r2-d2 |
∴
| 17 |
5-(
|
| 3 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.
.设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.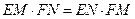 ;
;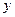 轴上,半径为1,且过点(1,2)的圆的方程为( )
轴上,半径为1,且过点(1,2)的圆的方程为( )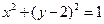
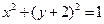
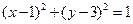

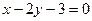 与圆
与圆 交于
交于 两点,则
两点,则
 (
(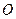 是
是