题目内容
17.某地最近十年粮食需求量逐年上升,下表是部分统计数据:| 年份x | 2006 | 2008 | 2010 | 2012 | 2014 |
| 需求量y(万吨) | 240 | 255 | 260 | 265 | 280 |
(Ⅱ)如果x,y线性相关,利用所给数据求x,y之间的回归直线方程$y=\hat bx+\hat a$;
(Ⅲ)利用(Ⅱ)中所求出的直线方程预测该地2015年的粮食需求量.
(参考公式:线性回归方程系数公式$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}$,$\hat a=\bar y-\hat b\bar x$,
线性相关系数公式$r=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sqrt{(\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2})(\sum_{i=1}^n{{y_i}^2-n{{\overline y}^2}})}}}}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y})}}{{\sqrt{(\sum_{i=1}^n{{{({x_i}-\overline x)}^2})(\sum_{i=1}^n{{{({y_i}-\overline y)}^2})}}}}}$,
相关性检验临界值表:
| P(K2≥k0) | 小概率 | |
| 0.05 | 0.01 | |
| k0 | 0.878 | 0.959 |
分析 (Ⅰ)根据所给的数据利用最小二乘法.公式计算得r,查表得r0.01=0.959,最后得出需求量与年份两者之间存在线性相关关系.
(Ⅱ)写出线性回归方程的系数和a的值,写出线性回归方程,注意运算过程中不要出错;
(Ⅲ)将x=2015代入可预测该地2015年的粮食需求量.
解答 解:(Ⅰ)由已知中的数据可得:$\overline{x}$=2010,$\overline{y}$=260,
故r=$\frac{\sum _{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{(\sum _{i=1}^{5}{({x}_{i}-\overline{x})}^{2})(\sum _{i=1}^{5}{({y}_{i}-\overline{y})}^{2})}}$=$\frac{180}{10\sqrt{340}}$≈0.976;
查表得r0.01=0.959,
∵0.976>0.959,
∴需求量与年份两者之间存在线性相关关系.
(Ⅱ)由已知中的数据可得:$\widehat{b}=\frac{\sum _{i=1}^{5}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum _{i=1}^{5}{({x}_{i}-\overline{x})}^{2}}$=$\frac{180}{40}$=$\frac{9}{2}$,
∴$\hat a=\bar y-\hat b\bar x$=260-2010×$\frac{9}{2}$=-8785,
∴x,y之间的回归直线方程$\hat{y}$=$\frac{9}{2}$x-8785,
(Ⅲ)由(Ⅱ)中$\hat{y}$=$\frac{9}{2}$x-8785得:
当x=2015时,$\hat{y}$=282.5,
即预测该地2015年的粮食需求量约为282.5万吨.
点评 本题考查线性回归方程,是一个中档题,解题的关键是利用最小二乘法写出线性回归系数,注意解题的运算过程不要出错.

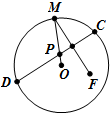 如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )
如图,圆心为O的圆形纸片内有一个定点F(点F与点O不重合),点M在圆周上,现把纸片折叠让点M与点F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,当点M在圆周上运动时,点P形成的轨迹是( )