题目内容
（几何证明选讲选做题）在梯形
中，
，
，
，点
、
分别在
、
上，且
，若
，则
的长为 ．
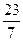
解析
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
，面SCD与面SAB所成二面角的正切值为 
。
中，
.若二面角
的大小为
，则点
到平面
的距离为 。 
，若
，且
与
相交但不垂直，直线
分别为
；②任意
； ③存在
； ④存在
； ⑤任意
； ⑥存在
。真命题的序号是_________ 。平面上的点
的距离是( )
A． | B． | C． | D．40 |
第1卷单元月考期中期末系列答案题目内容
（几何证明选讲选做题）在梯形中，，，，点、分别在、上，且，若，则的长为 ．
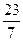
解析
第1卷单元月考期中期末系列答案平面上的点的距离是( )
| A． | B． | C． | D．40 |
，m，n是直线. 给出下列命题： 
，则α⊥β
为直角三角形，∠ACB＝90°，AC＝6，BC＝CC1＝
，P是BC1上一动点，则CP＋PA1的最小值是___________；