题目内容
如右下图所示,点S在平面ABC外,SB⊥AC,SB=AC=2, E、F分别是SC和AB的中点,则EF=________. 
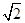
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如右下图所示,点S在平面ABC外,SB⊥AC,SB=AC=2, E、F分别是SC和AB的中点,则EF=________. 
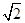
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案