题目内容
(2007•天津一模)一个棱锥的三个侧面中有两个是等腰直角三角形,另一个是边长为1的正三角形,这样的三棱锥体积为
(
或
或
)
| ||
| 24 |
| ||
| 12 |
| ||
| 12 |
(
或
或
)
.(写出一个可能值)
| ||
| 24 |
| ||
| 12 |
| ||
| 12 |
分析:由题意画出棱锥的不同情况,然后分别求出几何体的体积即可.
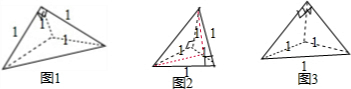
解答:解:如图1,两个侧面是等腰三角形,一个侧面是正三角形,三棱锥的体积是:
×
×1×1×sin60°×1=
.
如图2:底面是正三角形,一个侧面是正三角形,另2个侧面是直角三角形,
它的体积是两个三棱锥的体积的和,即
×
×
×
×1=
.
如图3,三棱锥的底面是正三角形,3个侧面都是等腰直角三角形,它的体积是:
×
×
×
×
=
;
故答案为:
或
或
.
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 12 |
如图2:底面是正三角形,一个侧面是正三角形,另2个侧面是直角三角形,
它的体积是两个三棱锥的体积的和,即
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 12 |
如图3,三棱锥的底面是正三角形,3个侧面都是等腰直角三角形,它的体积是:
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 24 |
故答案为:
| ||
| 24 |
| ||
| 12 |
| ||
| 12 |

点评:本题是基础题,考查棱锥的体积的求法,考查空间想象能力,计算能力,分类讨论思想,容易漏掉不同的情况.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 (2007•天津一模)如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
(2007•天津一模)如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.