题目内容
 (2007•天津一模)如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
(2007•天津一模)如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.(1)求点B到平面A1C1CA的距离;
(2)求二面角B-A1D-A的大小;
(3)在线段AC上是否存在一点F,使得EF⊥平面A1BD?若存在,确定其位置并证明结论;若不存在,说明理由.
分析:(1)由直棱柱的定义结合线面垂直的性质与判定,证出BC⊥平面A1C1CA,从而BC长即为B点到平面A1C1CA的距离,结合题意得到点B到平面A1C1CA的距离为2;
(2)分别以AB、CA、CC1为x、y、z轴,建立如图所示的空间直角坐标系,可得C、B、A、C1、B1、A1、D和E点的坐标,从而得到
、
的坐标,利用垂直向量数量积为零的方法建立方程组解出
=(1,-1,2)是平面A1BD的一个法向量,结合
=(1,0,0)是平面ACC1A1的一个法向量,利用空间向量的夹角公式即可算出二面角B-A1D-A的大小;
(3)设F(0,y,0)使得EF⊥平面A1BD,利用(2)的结论得此时
∥
,算出
=(1,-y,2)并利用向量平行的条件解出y=1,从而得到存在线段AC的中点F,使得EF⊥平面A1BD.
(2)分别以AB、CA、CC1为x、y、z轴,建立如图所示的空间直角坐标系,可得C、B、A、C1、B1、A1、D和E点的坐标,从而得到
| BD |
| BA1 |
| n |
| m |
(3)设F(0,y,0)使得EF⊥平面A1BD,利用(2)的结论得此时
| n |
| FE |
| EF |
解答:解:(1)∵A1B1C1-ABC为直三棱住,
∴CC1⊥底面ABC,结合BC?底面ABC,可得CC1⊥BC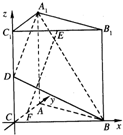
∵AC⊥CB,AC、CC1是平面A1C1CA内的相交直线
∴BC⊥平面A1C1CA…(2分)
可得BC长即为B点到平面A1C1CA的距离
结合BC=2可得点B到平面A1C1CA的距离为2…(4分)
(2)∵A1B1C1-ABC为直三棱住,C1C=CB=CA=2,
AC⊥CB,D、E分别为C1C、B1C1的中点
∴分别以AB、CA、CC1为x、y、z轴,建立如图所示的空间直角坐标系,
得C(0,0,0),B(2,0,0),A(0,2,0),C1(0,0,2),
B1(2,0,2),A1(0,2,2),D(0,0,1),E(1,0,2)…(6分)
∴
=
设平面A1BD的法向量为
=(1,λ,μ)
可得
,即
,解之得λ=-1、μ=2
∴
=(1,-1,2)…(8分)
又∵
=(1,0,0)是平面ACC1A1的一个法向量,
∴由cos<
,
>=
=
,可得二面角B-A1D-A的大小为arccos
…(10分)
(3)在线段AC上存在一点F,设F(0,y,0)使得EF⊥平面A1BD…(11分)
根据(2)的结论可知,当且仅当
∥
时EF⊥平面A1BD,…(12分)
∵
=(1,-y,2),可得y=1…(13分)
∴存在唯一的一个点F(0,1,0),即AC中点满足条件
综上所述,存在线段AC的中点F,使得EF⊥平面A1BD…(14分)
∴CC1⊥底面ABC,结合BC?底面ABC,可得CC1⊥BC

∵AC⊥CB,AC、CC1是平面A1C1CA内的相交直线
∴BC⊥平面A1C1CA…(2分)
可得BC长即为B点到平面A1C1CA的距离
结合BC=2可得点B到平面A1C1CA的距离为2…(4分)
(2)∵A1B1C1-ABC为直三棱住,C1C=CB=CA=2,
AC⊥CB,D、E分别为C1C、B1C1的中点
∴分别以AB、CA、CC1为x、y、z轴,建立如图所示的空间直角坐标系,
得C(0,0,0),B(2,0,0),A(0,2,0),C1(0,0,2),
B1(2,0,2),A1(0,2,2),D(0,0,1),E(1,0,2)…(6分)
∴
| BD |
|
设平面A1BD的法向量为
| n |
可得
|
|
∴
| n |
又∵
| m |
∴由cos<
| m |
| n |
| 1 | ||
|
| ||
| 6 |
| ||
| 6 |
(3)在线段AC上存在一点F,设F(0,y,0)使得EF⊥平面A1BD…(11分)
根据(2)的结论可知,当且仅当
| n |
| FE |
∵
| EF |
∴存在唯一的一个点F(0,1,0),即AC中点满足条件
综上所述,存在线段AC的中点F,使得EF⊥平面A1BD…(14分)
点评:本题在三棱柱中求点到平面的距离、证明线面垂直并求二面角的大小.着重考查了直棱柱的性质、利用空间向量的方法探索线面垂直和求面面角等知识,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目