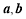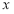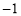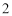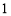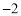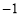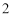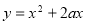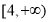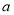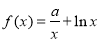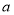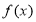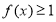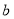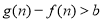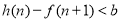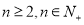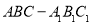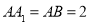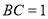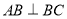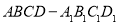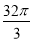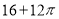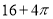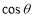题目内容
已知一条曲线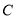 在
在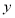 轴右侧,
轴右侧,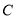 上每一点到点
上每一点到点 的距离减去它到
的距离减去它到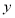 轴距离的差都是1.
轴距离的差都是1.
(1)求曲线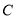 的方程;
的方程;
(2)设直线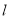 交曲线
交曲线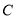 于
于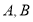 两点,线段
两点,线段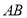 的中点为
的中点为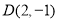 ,求直线
,求直线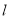 的一般式方程.
的一般式方程.
(1)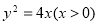 ;(2)
;(2)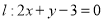 .
.
【解析】
试题分析:(1)设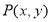 是曲线
是曲线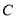 上任意一点,利用两点之间的距离公式建立关于
上任意一点,利用两点之间的距离公式建立关于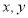 的方程,化简即为曲线
的方程,化简即为曲线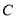 的方程;(2)设
的方程;(2)设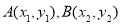 ,然后利用点差法,结合中点坐标公式与斜率进行转换即可求得直线的斜率,最后利用点斜式,通过化简可求得直线
,然后利用点差法,结合中点坐标公式与斜率进行转换即可求得直线的斜率,最后利用点斜式,通过化简可求得直线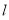 的一般式方程.
的一般式方程.
试题解析:(1)设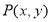 是曲线
是曲线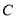 上任意一点,那么点
上任意一点,那么点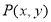 满足:
满足:
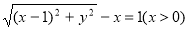 ,化简得
,化简得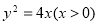 .
.
(2)设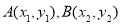 ,由
,由 ,
,
① ②得:
②得: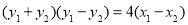 ,由于易知
,由于易知 的斜率
的斜率 存在,
存在,
故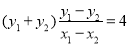 ,即
,即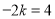 ,所以
,所以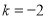 ,故
,故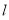 的一般式方程为
的一般式方程为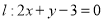 .
.
考点:1、抛物线方程的求法;2、直线与抛物线的位置关系;3、点差法的应用.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目