题目内容
设
(1)求 的表达式,并判断
的表达式,并判断 的奇偶性;
的奇偶性;
(2)试证明:函数 的图象上任意两点的连线的斜率大于0;
的图象上任意两点的连线的斜率大于0;
(3)对于 ,当
,当 时,恒有
时,恒有 求m的取值范围。
求m的取值范围。
(1)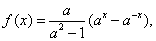 奇函数
奇函数
(2)当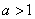 时,
时,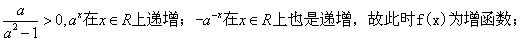
当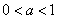 时,
时,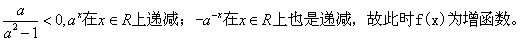 综上,
综上, 为增函数,由增函数的定义知:
为增函数,由增函数的定义知: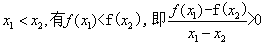 ,
,
故任意两点的连线斜率都大于零。(3)1<m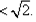
解析试题分析:(1)令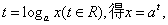 代入
代入 中,得
中,得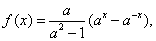
 的定义域为R,关于原点对称。
的定义域为R,关于原点对称。

(2)当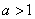 时,
时,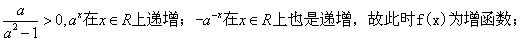
当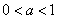 时,
时,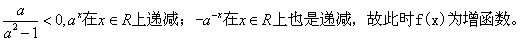 综上,
综上, 为增函数,由增函数的定义知:
为增函数,由增函数的定义知: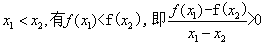 ,
,
故任意两点的连线斜率都大于零。
(3)由(1)知 为奇函数,由(2)知
为奇函数,由(2)知 在
在 为增函数,故有
为增函数,故有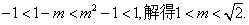
考点:本题考查了函数的性质的综合运用
点评:函数的单调性、奇偶性、周期性通常用于求解函数中的参数以及参数的范围,利用函数的性质往往能使问题简化

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目

 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;(3)若函数y=f(x)的图象上任意不同的两点的连线的斜率小于1,求证
的充要条件;(3)若函数y=f(x)的图象上任意不同的两点的连线的斜率小于1,求证 。
。 在
在 处取得极小值2.
处取得极小值2. 的解析式;
的解析式; ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围. (
( 且
且 ).
). 的定义域;
的定义域; 的
的 取值范围.
取值范围. ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的 ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的 .
. ∈R,函数
∈R,函数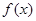 =
=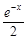 (
(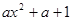 ),其中e是自然对数的底数.
),其中e是自然对数的底数. ,若存在x0∈R,使方程
,若存在x0∈R,使方程 成立,则称x0为
成立,则称x0为 (a≠0).
(a≠0). 时,求函数
时,求函数
 有三个不同的实根.
有三个不同的实根. 为奇函数,且在
为奇函数,且在 上为增函数,
上为增函数,  , 若
, 若 对所有
对所有 都成立,求
都成立,求 的取值范围。
的取值范围。