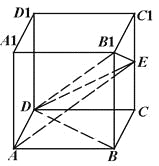
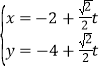ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΦΉΘ§““ΝΫΧ®Μζ¥≤Ά§ ±…ζ≤ζ“Μ÷÷ΝψΦΰΘ§Τδ÷ ΝΩΑ¥≤β ‘÷Η±ξΜ°Ζ÷ΘΚ÷Η±ξ¥σ”ΎΜρΒ»”Ύ100ΈΣ”≈ΤΖΘ§¥σ”ΎΒ»”Ύ90«“–Γ”Ύ100ΈΣΚœΗώΤΖΘ§–Γ”Ύ90ΈΣ¥ΈΤΖΘ§œ÷ΥφΜζ≥ι»Γ’βΝΫΧ®≥Β¥≤…ζ≤ζΒΡΝψΦΰΗς100ΦΰΫχ––Φλ≤βΘ§Φλ≤βΫαΙϊΆ≥ΦΤ»γœ¬ΘΚ
≤β ‘÷Η±ξ | [85Θ§90Θ© | [90Θ§95Θ© | [95Θ§100Θ© | [100Θ§105Θ© | [105Θ§110Θ© |
Μζ¥≤ΦΉ | 8 | 12 | 40 | 32 | 8 |
Μζ¥≤““ | 7 | 18 | 40 | 29 | 6 |
Θ®1Θ© ‘Ζ÷±πΙάΦΤΦΉΜζ¥≤ΓΔ““Μζ¥≤…ζ≤ζΒΡΝψΦΰΈΣ”≈ΤΖΒΡΗ≈¬ ΘΜ
Θ®2Θ©ΦΉΜζ¥≤…ζ≤ζ“ΜΦΰΝψΦΰΘ§»τ «”≈ΤΖΩ…”·άϊ160‘ΣΘ§ΚœΗώΤΖΩ…”·άϊ100‘ΣΘ§¥ΈΤΖ‘ρΩςΥπ20‘ΣΘΜΦΌ…ηΦΉΜζ¥≤Ρ≥Χλ…ζ≤ζ50ΦΰΝψΦΰΘ§«κΙάΦΤΦΉΜζ¥≤ΗΟΧλΒΡ»’άϊ»σΘ®ΒΞΈΜΘΚ‘ΣΘ©ΘΜ
Θ®3Θ©¥”ΦΉΓΔ““Μζ¥≤…ζ≤ζΒΡΝψΦΰ÷Η±ξ‘Ύ[90Θ§95Θ©ΡΎΒΡΝψΦΰ÷–Θ§≤…”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»Γ5ΦΰΘ§¥”’β5Φΰ÷–»Έ―Γ2ΦΰΫχ––÷ ΝΩΖ÷ΈωΘ§«σ’β2ΦΰΕΦ «““Μζ¥≤…ζ≤ζΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ®2Θ©5720Θ®3Θ©
Θ®2Θ©5720Θ®3Θ©![]()
ΓΨΫβ¥πΓΩΫβΘΚΘ®1Θ©“ρΈΣΦΉΜζ¥≤ΈΣ”≈ΤΖΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
““Μζ¥≤ΈΣ”≈ΤΖΒΡΤΒ¬ ‘ΦΈΣ![]() Θ§
Θ§
Υυ“‘ΙάΦΤΦΉΓΔ““ΝΫΜζ¥≤ΈΣ”≈ΤΖΒΡΗ≈¬ Ζ÷±πΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΦΉΜζ¥≤±Μ≥ι≤ζΤΖΟΩ1ΦΰΒΡΤΫΨυ ΐάϊ»σΈΣΘΚ
![]() ‘Σ
‘Σ
Υυ“‘ΙάΦΤΦΉΜζ¥≤ΟΩ…ζ≤ζ1ΦΰΒΡάϊ»σΈΣ114.4‘Σ
Υυ“‘ΦΉΜζ¥≤Ρ≥Χλ…ζ≤ζ50ΦΰΝψΦΰΒΡάϊ»σΈΣ50ΓΝ114.4=5720‘Σ
Θ®3Θ©”…Χβ“β÷ΣΘ§ΦΉΜζ¥≤”Π≥ι»Γ![]() Θ§
Θ§
““Μζ¥≤”Π≥ι»Γ![]() Θ§
Θ§
Φ«ΦΉΜζ¥≤ΒΡ2ΗωΝψΦΰΈΣAΘ§BΘ§““Μζ¥≤ΒΡ3ΗωΝψΦΰΈΣaΘ§bΘ§cΘ§
»τ¥”5Φΰ÷–―Γ»Γ2ΦΰΖ÷±πΈΣABΘ§AaΘ§AbΘ§AcΘ§BaΘ§BbΘ§BcΘ§abΘ§acΘ§bcΙ≤10÷÷»ΓΖ®
¬ζΉψΧθΦΰΒΡΙ≤”–3÷÷Θ§Ζ÷±πΈΣabΘ§acΘ§bcΘ§
Υυ“‘Θ§’β2ΦΰΕΦ «““Μζ¥≤…ζ≤ζΒΡΗ≈¬ ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷Έω:Θ®1Θ©ΗυΨίΤΒ ΐ≥ΐ“‘Ήή ΐΦΤΥψΤΒ¬ Θ§ΫχΕχΙάΦΤΗ≈¬ Θ®2Θ©œ»ΗυΨίΤΒ¬ ΦΤΥψ”≈ΤΖΘ§ΚœΗώΤΖΘ§¥ΈΤΖΥυΕ‘”ΠΗ≈¬ Θ§‘Ό”κΕ‘”Πάϊ»σœύ≥ΥΒΡΚΆΈΣΥυ«σΘ®3Θ©œ»ΗυΨίΖ÷≤ψ≥ι―υ»ΖΕ®ΦΉ2““3Θ§άϊ”ΟΟΕΨΌΖ®»ΖΕ® ¬ΦΰΉή ΐΘ§¥”÷–»ΖΕ®2ΦΰΕΦ «““Μζ¥≤ΒΡΜυ±Ψ ¬Φΰ ΐΘ§ΉνΚσΗυΨίΙ≈ΒδΗ≈–ΆΗ≈¬ ΙΪ Ϋ«σΗ≈¬
‘ΧβΫβΈω:ΫβΘΚΘ®1Θ©“ρΈΣΦΉΜζ¥≤ΈΣ”≈ΤΖΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
““Μζ¥≤ΈΣ”≈ΤΖΒΡΤΒ¬ ‘ΦΈΣ![]() Θ§
Θ§
Υυ“‘ΙάΦΤΦΉΓΔ““ΝΫΜζ¥≤ΈΣ”≈ΤΖΒΡΗ≈¬ Ζ÷±πΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΦΉΜζ¥≤±Μ≥ι≤ζΤΖΟΩ1ΦΰΒΡΤΫΨυ ΐάϊ»σΈΣΘΚ
![]() ‘Σ
‘Σ
Υυ“‘ΙάΦΤΦΉΜζ¥≤ΟΩ…ζ≤ζ1ΦΰΒΡάϊ»σΈΣ114.4‘Σ
Υυ“‘ΦΉΜζ¥≤Ρ≥Χλ…ζ≤ζ50ΦΰΝψΦΰΒΡάϊ»σΈΣ50ΓΝ114.4=5720‘Σ
Θ®3Θ©”…Χβ“β÷ΣΘ§ΦΉΜζ¥≤”Π≥ι»Γ![]() Θ§
Θ§
““Μζ¥≤”Π≥ι»Γ![]() Θ§
Θ§
Φ«ΦΉΜζ¥≤ΒΡ2ΗωΝψΦΰΈΣAΘ§BΘ§““Μζ¥≤ΒΡ3ΗωΝψΦΰΈΣaΘ§bΘ§cΘ§
»τ¥”5Φΰ÷–―Γ»Γ2ΦΰΖ÷±πΈΣABΘ§AaΘ§AbΘ§AcΘ§BaΘ§BbΘ§BcΘ§abΘ§acΘ§bcΙ≤10÷÷»ΓΖ®
¬ζΉψΧθΦΰΒΡΙ≤”–3÷÷Θ§Ζ÷±πΈΣabΘ§acΘ§bcΘ§
Υυ“‘Θ§’β2ΦΰΕΦ «““Μζ¥≤…ζ≤ζΒΡΗ≈¬ ![]() Θ°
Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ