题目内容
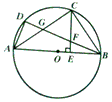
如图,已知AB是圆O的直径,C,D是圆上两点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG,
(1)求证:C是弧BD的中点;
(2)求证:BF=FG。
(1)求证:C是弧BD的中点;
(2)求证:BF=FG。
证明:(1) ,
,
∴ ,
,
∵AB为圆O的直径,
∴ ,
,
∵CE⊥AB,
∴ ,
,
∴ ,
, ,
,
∴ ,
,
∴弧BC=弧CD,
∴C为弧BD的中点。
(2) ,
, ,
,
∴ ,
,
由(1) ,
,
∴ ,
,
∴CF=BF,
∵CF=FG,
∴BF=FG。
 ,
,∴
 ,
,∵AB为圆O的直径,
∴
 ,
,∵CE⊥AB,
∴
 ,
,∴
 ,
, ,
,∴
 ,
,∴弧BC=弧CD,
∴C为弧BD的中点。
(2)
 ,
, ,
,∴
 ,
,由(1)
 ,
,∴
 ,
,∴CF=BF,
∵CF=FG,
∴BF=FG。

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
 (2013•西城区一模)如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为
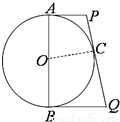
(2013•西城区一模)如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为 (2011•东城区模拟)如图,已知AB是圆O的直径,AB=4,C为圆上任意一点,过C点做圆的切线分别与过A,B两点的切线交于P,Q点,则CP•CQ=
(2011•东城区模拟)如图,已知AB是圆O的直径,AB=4,C为圆上任意一点,过C点做圆的切线分别与过A,B两点的切线交于P,Q点,则CP•CQ=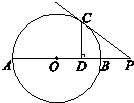 如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为________;BP=________.
如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为________;BP=________.