题目内容
如图,已知AB是圆O的直径,AB=4,C为圆上任意一点,过C点做圆的切线分别与过A,B两点的切线交于P,Q点,则CP•CQ= .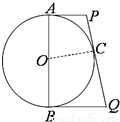
【答案】分析:连接OP,OQ,先证明△OAP≌△OCP,可得∠AOP=∠COP,同理,∠COQ=∠BOQ,所以∠POQ=90°,再证明△OCP∽△QCO
,可得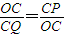 ,从而CP•CQ=OC2,故可解.
,从而CP•CQ=OC2,故可解.
解答:解:连接OP,OQ,
∵PA,PC为圆O的切线,
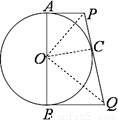
∴PA=PC
在△OAP和△OCP中
∵PA=PC,OP=OP,OA=OC
∴△OAP≌△OCP
∴∠AOP=∠COP
同理,∠COQ=∠BOQ
∴∠POQ=90°
∵OC⊥PQ
∴△OCP∽△QCO
∴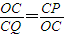
∴CP•CQ=OC2
∵AB=4,
∴OC=2
∴CP•CQ=4
故答案为:4
点评:本题以圆为载体,考查圆的切线,考查三角形的全等与相似,解题的关键是正确运用圆的切线的性质.
,可得
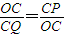 ,从而CP•CQ=OC2,故可解.
,从而CP•CQ=OC2,故可解.解答:解:连接OP,OQ,
∵PA,PC为圆O的切线,

∴PA=PC
在△OAP和△OCP中
∵PA=PC,OP=OP,OA=OC
∴△OAP≌△OCP
∴∠AOP=∠COP
同理,∠COQ=∠BOQ
∴∠POQ=90°
∵OC⊥PQ
∴△OCP∽△QCO
∴
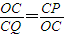
∴CP•CQ=OC2
∵AB=4,
∴OC=2
∴CP•CQ=4
故答案为:4
点评:本题以圆为载体,考查圆的切线,考查三角形的全等与相似,解题的关键是正确运用圆的切线的性质.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 (2013•西城区一模)如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为
(2013•西城区一模)如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为 (2011•东城区模拟)如图,已知AB是圆O的直径,AB=4,C为圆上任意一点,过C点做圆的切线分别与过A,B两点的切线交于P,Q点,则CP•CQ=
(2011•东城区模拟)如图,已知AB是圆O的直径,AB=4,C为圆上任意一点,过C点做圆的切线分别与过A,B两点的切线交于P,Q点,则CP•CQ=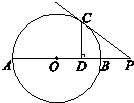 如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为________;BP=________.
如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为________;BP=________.