题目内容
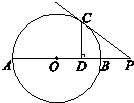 如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为________;BP=________.
如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为________;BP=________.
 5
5分析:连接OC.设圆的半径为R.由切线PC,可得OC⊥PC,又CD⊥OP,由“等积变形”即可得出
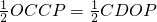 ,再利用切割线定理可得PC2=PB•PA,联立解出即可.
,再利用切割线定理可得PC2=PB•PA,联立解出即可.解答:连接OC.设圆的半径为R.
∵PC切圆O于点C,∴OC⊥CP.
又∵CD⊥OP,
在Rt△OCP中,
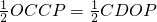 ,CD=6,CP=10,
,CD=6,CP=10,∴10R=6(R+PB).
由切割线定理可得:PC2=PB•PA,
∴102=PB•(PB+2R).
联立
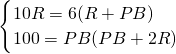 ,解得
,解得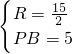 .
.因此⊙O的半径为
 ,PB=5.
,PB=5.故答案分别为
 ,5.
,5.点评:熟练掌握圆的切线性质、切割线定理、“等积变形”是解题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 (2013•西城区一模)如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为
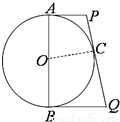
(2013•西城区一模)如图,已知AB是圆O的直径,P在AB的延长线上,PC切圆O于点C,CD⊥OP于D.若CD=6,CP=10,则圆O的半径长为 (2011•东城区模拟)如图,已知AB是圆O的直径,AB=4,C为圆上任意一点,过C点做圆的切线分别与过A,B两点的切线交于P,Q点,则CP•CQ=
(2011•东城区模拟)如图,已知AB是圆O的直径,AB=4,C为圆上任意一点,过C点做圆的切线分别与过A,B两点的切线交于P,Q点,则CP•CQ=