题目内容
等差数列{an}中,a4+a10+a16=30,则a18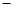 2a14的值为 ( )
2a14的值为 ( )
A.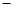 20 20 | B.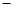 10 10 | C.10 | D.20 |
B
解析试题分析:因为a4+a10+a16=30,所以a10=10,又a18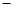 2a14=
2a14=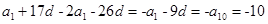 。
。
考点:本题考查等差数列的性质;等差数列的通项公式。
点评:根据已知条件和等差数列的性质,求出a10的值,是解答本题的关键,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知等差数列 的前
的前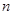 项和为
项和为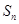 ,且满足
,且满足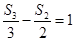 ,则数列
,则数列 的公差是( )
的公差是( )
A. | B.1 | C.2 | D.3 |
在△ABC中,tanA是以 为第3项,4为第7项的等差数列的公差;tanB是以
为第3项,4为第7项的等差数列的公差;tanB是以 为第3
为第3
项,9为第6项的等比数列的公比,则该三角形为 ( )
| A.等腰三角形 | B.锐角三角形 |
| C.直角三角形 | D.钝角三角形 |
已知等差数列40,37,34,……前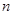 项和为
项和为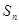 ,则使
,则使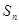 最大的正整数
最大的正整数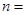 ( )
( )
| A.12 | B.13 | C.14 | D.15 |
已知等差数列{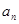 }的前2006项的和
}的前2006项的和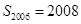 ,其中所有的偶数项的和是2,则
,其中所有的偶数项的和是2,则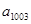 的值为( )
的值为( )
| A.1 | B.2 | C.3 | D.4 |
在等差数列 中,已知
中,已知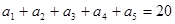 ,那么
,那么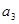 =
=
| A.3 | B.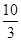 | C.4 | D.5 |
已知等差数列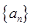 的通项公式
的通项公式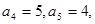 ,则
,则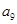 等于( )
等于( )
| A.1 | B.2 | C.0 | D.3 |
等差数列 中,若
中,若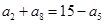 ,则
,则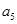 等于
等于
| A.3 | B.4 | C.5 | D.6 |
已知等差数列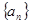 的公差为
的公差为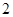 ,若
,若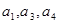 成等比数列, 则
成等比数列, 则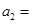 ( )
( )
A.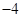 | B.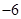 | C.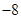 | D.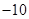 |