题目内容
已知等差数列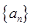 的通项公式
的通项公式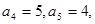 ,则
,则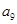 等于( )
等于( )
| A.1 | B.2 | C.0 | D.3 |
C
解析试题分析: 由于等差数列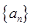 的通项公式中,
的通项公式中,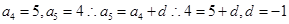 ,而结合通项公式的性质有
,而结合通项公式的性质有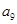 =
=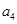 +5d=5+5
+5d=5+5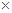 (-1)=0,故选C。
(-1)=0,故选C。
考点:本题主要考查了等差数列的通项公式的运用。
点评:解决该试题的关键是能够熟练的运用通项公式的性质,联立方程组得到首项和公差,进而得到第n项的值。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知等差数列{an}满足a2=3,Sn-Sn-3=51(n>3) ,Sn= 100,则n的值为
| A.8 | B.9 | C.10 | D.11 |
设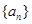 是等差数列,
是等差数列,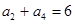 ,则这个数列的前5项和等于( )
,则这个数列的前5项和等于( )
| A.12 | B.13 | C.15 | D.18 |
等差数列{an}中,a4+a10+a16=30,则a18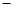 2a14的值为 ( )
2a14的值为 ( )
A.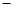 20 20 | B.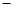 10 10 | C.10 | D.20 |
在等差数列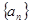 中,前四项之和为40,最后四项之和为80,所有项之和是210,则项数
中,前四项之和为40,最后四项之和为80,所有项之和是210,则项数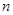 为( )
为( )
| A.12 | B.14 | C.15 | D.16 |
等差数列{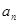 }中,
}中,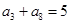 ,则前10项和
,则前10项和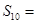 ( )
( )
| A.5 | B.25 | C.50 | D.100 |
已知数列{ } 是等差数列,且
} 是等差数列,且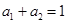 ,
,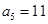 ,则数列{
,则数列{ }的前
}的前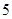 项的和
项的和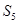 等于( )
等于( )
A. | B.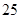 | C.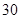 | D.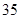 |
等差数列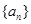 的前n项和为
的前n项和为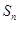 ,且
,且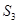 =6,
=6,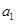 =4, 则公差d等于 ( )
=4, 则公差d等于 ( )
| A.1 | B.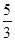 | C.- 2 | D.3 |
在等差数列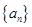 中,
中,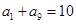 ,则
,则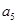 的值为( )
的值为( )
| A.5 | B.6 | C.8 | D.10 |