题目内容
已知等差数列40,37,34,……前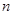 项和为
项和为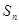 ,则使
,则使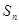 最大的正整数
最大的正整数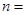 ( )
( )
| A.12 | B.13 | C.14 | D.15 |
C
解析试题分析:由题意知,数列的首项是40,公差为-3的等差数列,所以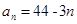 ,由
,由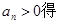 :
: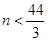 ,所以使
,所以使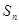 最大的正整数
最大的正整数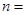 14.
14.
考点:本题考查等差数列的前n项和;等差数列的通项公式。
点评:直接考查等差数列的前n项和公式,属于基础题型。

练习册系列答案
相关题目
已知数列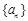 是公比为q的等比数列,且
是公比为q的等比数列,且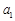 ,
,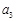 ,
,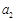 成等差数列,则q=
成等差数列,则q=
A.1或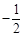 | B.1 | C.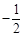 | D.-2 |
设数列 的前n项和为
的前n项和为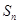 ,令
,令 ,称
,称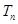 为数列
为数列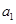 ,
,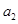 ,……,
,……,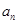 的“理想数”,已知数列
的“理想数”,已知数列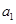 ,
,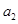 ,……,
,……,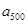 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 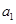 ,
,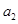 ,……,
,……,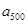 的“理想数”为( )
的“理想数”为( )
| A.2002 | B.2004 | C.2006 | D.2008 |
已知数列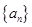 的前n项和
的前n项和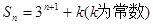 ,那么下述结论正确的是( )
,那么下述结论正确的是( )
A.k为任意实数时,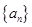 是等比数列 是等比数列 |
B.k =-3时,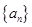 是等比数列 是等比数列 |
C.k =-1时,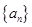 是等比数列 是等比数列 |
D.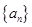 不可能等比数列 不可能等比数列 |
设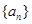 是等差数列,
是等差数列,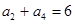 ,则这个数列的前5项和等于( )
,则这个数列的前5项和等于( )
| A.12 | B.13 | C.15 | D.18 |
已知等差数列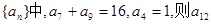 的值是( )
的值是( )
| A.30 | B.15 | C.31 | D.64 |
等差数列{an}中,a4+a10+a16=30,则a18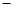 2a14的值为 ( )
2a14的值为 ( )
A.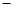 20 20 | B.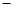 10 10 | C.10 | D.20 |
等差数列{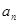 }中,
}中,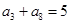 ,则前10项和
,则前10项和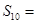 ( )
( )
| A.5 | B.25 | C.50 | D.100 |
等差数列{an}中,已知a1=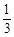 ,a2+a5=4,an=33,则n的值为( ).
,a2+a5=4,an=33,则n的值为( ).
| A.50 | B.49 | C.48 | D.47 |