题目内容
已知复数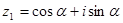 ,
, 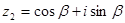 ,
, 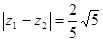 ,求:(1)求
,求:(1)求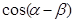 的值; (2)若
的值; (2)若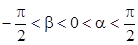 ,且
,且 ,求
,求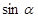 的值.
的值.
(1)cos(α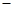 β)=
β)=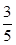 (2)
(2)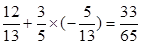
解析试题分析:解:(1)∵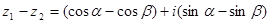 ,
,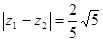 ,
,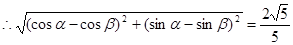 ,∴cos(α
,∴cos(α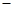 β)=
β)= .
.
(2)∵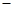
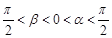 ,∴0<α-β<π,由(1)得cos(α
,∴0<α-β<π,由(1)得cos(α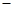 β)=
β)=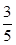 ,
,
∴sin(α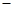 β)=
β)=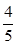 . 又sinβ=
. 又sinβ=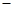
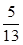 ,∴cosβ=
,∴cosβ= 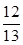 .
.
∴sinα=sin[(α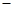 β)+β]=sin(α
β)+β]=sin(α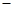 β)cosβ+cos(α
β)cosβ+cos(α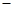 β)sinβ=
β)sinβ=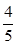 ×
×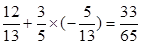 .
.
考点:三角恒等变换
点评:解决的关键是能结合两角和差的公式来求解函数的值,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
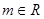 ,复数
,复数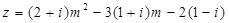 ,
,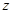 的代数形式;
的代数形式;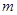 为何值时,
为何值时,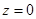 ?当
?当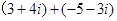 ; (2)
; (2)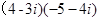 ;
;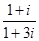 ; (4)
; (4)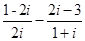
 ,复数
,复数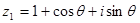 ,
,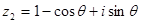 .
.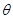 取何值时,
取何值时,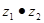 是实数;
是实数;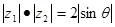 .
. +2iz=8+ai (a∈R),试求a的取值范围.
+2iz=8+ai (a∈R),试求a的取值范围.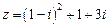 .
.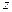 及
及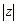 ;
;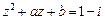 ,求实数
,求实数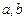 的值.
的值. -(3-2i)
-(3-2i) x-6i="0." (1)若x∈R,求x的值. (2)若x∈C,求x的值.
x-6i="0." (1)若x∈R,求x的值. (2)若x∈C,求x的值.  =(a+2z)2.
=(a+2z)2. ,且以下命题都为真命题:
,且以下命题都为真命题: 实系数一元二次方程
实系数一元二次方程 的两根都是虚数;
的两根都是虚数; 存在复数
存在复数 同时满足
同时满足 且
且 .
. 的取值范围.
的取值范围.