在等差数列{an}中a1=-2015.其前n项和为Sn.若2S6-3S4=24.则S2015=( )A．-2014B．2014C．2015D．-2015 题目和参考答案——青夏教育精英家教网—

题目内容

7．在等差数列{a_n}中a₁=-2015，其前n项和为S_n，若2S₆-3S₄=24，则S₂₀₁₅=（　　）

A．

-2014

B．

2014

C．

2015

D．

-2015

分析由已知条件和等差数列的求和公式可得d的方程，解方程代入求和公式可得．

解答解：设等差数列{a_n}的公差为d，
由题意可得2S₆-3S₄=2（6a₁+$\frac{6×5}{2}$d）-3（4a₁+$\frac{4×3}{2}$d）=12d=24，
解得d=2，又a₁=-2015，
∴S₂₀₁₅=2015a₁+$\frac{2015×2014}{2}$d=-2015²+2015×2014=-2015
故选：D

点评本题考查等差数列的求和公式，求出数列的公差是解决问题的关键，属基础题．

练习册系列答案

启东系列江苏省13大市中考真题汇编系列答案

18．i是虚数单位，复数$\frac{4-3i}{2+i}$=（　　）

15．设等差数列{a_n}的前n项和为A_n，等比数列{b_n}的前n项和为B_n，若a₃=b₃，a₄=b₄，且$\frac{{{A_5}-{A_3}}}{{{B_4}-{B_2}}}=7$，则数列{b_n}的公比q=-2．

2．如图所示是一个循环结构的算法，下列说法不正确的是（　　）

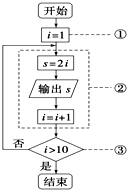
	A．	①是循环变量初始化，循环就要开始
	B．	②为循环体
	C．	③是判断是否继续循环的终止条件
	D．	输出的S值为2，4，6，8，10，12，14，16，18

12．已知函数$f（x）={（\sqrt{x}+\sqrt{2}）^2}$，（x≥0），又数列{a_n}中，a_n＞0，a₁=2，该数列的前n项和记为S_n，对所有大于1的自然数n都有S_n=f（S_n-1）．
（Ⅰ）求{a_n}的通项公式；
（Ⅱ）记b_n=$\frac{{{a_{n+1}}^2+{a_n}^2}}{{2{a_{n+1}}{a_n}}}$，{b_n}其前n项和为T_n，证明：T_n＜n+1．

19．正方体ABCD-A₁B₁C₁D₁的棱长为2，则三棱锥B-A₁B₁C₁公共部分的体积等于$\frac{4}{3}$．

16．

如图，点C是以AB为直径的圆O上不与A、B重合的一个动点，S是圆O所在平面外一点，且总有SC⊥平面ABC，M是SB的中点，AB=SC=2．
（Ⅰ）求证：OM⊥BC；
（Ⅱ）当四面体S-ABC的体积最大时，设直线AM与平面ABC所成的角为α，二面角B-SA-C的大小为β，分别求tanα，tanβ的值．

17．若变量x，y满足约束条件$\left\{\begin{array}{l}{y≤0}\\{x-2y≥1}\\{x-4y≤3}\end{array}\right.$，则z=3x+5y的最小值为（　　）

试题分类